I. (2sin²x - 7sinx + 3) · log₂ (x-8) = 0
ОДЗ : x-8 > 0; x > 8
Произведение равно нулю, когда один из множителей равен нулю.
1) 2sin²x - 7sinx + 3 = 0 - квадратное уравнение с неизвестным sinx
D = 7² - 4·2·3 = 25 = 5²
sin x = (7+5)/4 = 3 - не подходит под условие |sin x| ≤ 1
sin x = (7-5)/4 = 1/2
x₁ = π/6 + 2πn, n∈N, n≥2 ( ОДЗ: π/6 + 4π ≈ 13,1 > 8)
x₂ = 5π/6 + 2πk, k∈N ( ОДЗ: 5π/6 + 2π ≈ 8,9 > 8)
2) log₂ (x-8) = 0 ⇒ x - 8 = 2⁰
x = 1 + 8; x₃ = 9
==========================
II. x ∈ (3π; 6π)

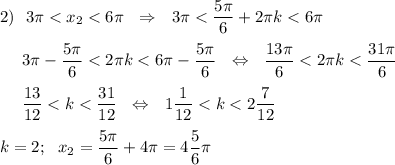
3) x₃ = 9 < 9,4 ≈ 3π - не входит в интервал
ответ:  ;
; 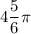
Если все двугранные углы при основании пирамиды равны, то высоты боковых граней равны между собой, а их проекции на основание - это радиусы r вписанной окружности в основание.
Отсюда ответ на первый вопрос:
вершина S пирамиды SABC проецируется в центр вписанной в основание пирамиды окружности.
Находим r = (a + b - c)/2.
Гипотенуза с = √(6² + 8²) = 10 см.
Тогда r = (6 + 8 - 10)/2 = 2 см.
Высота А боковой грани равна:
А = r/cos60° = 2/(1/2) = 4 см.
Периметр основания Р = 6+8+10 = 24 см.
Площадь боковой поверхности равна:
Sбок = (1/2)РА = (1/2)*24*4 = 48 см².
Площадь основания So = (1/2)ab = (1/2)*6*8 = 24 см².
ответ на второй вопрос: S = Sбок + So = 48 + 24 = 72 см².
x - 8 = 13n
x = 13n+8, где n∈N
Таким образом, для n=1, x = 13*1+8 = 21
для n=2, x = 13*2+8 = 34
для n=5, x = 13*5+8 = 73 и т.д.