ДАНО
Y = x²/(x² + 4)
ИССЛЕДОВАНИЕ
1.Область определения D(x) - непрерывная Х∈(-∞;+∞).
Вертикальных асимптот - нет.
2. Пересечение с осью Х. Y=0 при х = 0.
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.
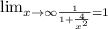
limY(+∞) = 1.
Горизонтальная асимптота - Y = 1.
5. Исследование на чётность.Y(-x) = Y(x).
Функция чётная.
6. Производная функции.
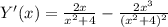
Корень при Х=0. Схема знаков производной.
(-∞)__(<0-убыв)__(х=0)_(<0-убыв)__(+∞)
7. Локальные экстремумы.
Максимума - нет, минимум – Ymin(0) = 0.
8. Интервалы монотонности.
Убывает - Х∈(-∞;0]. Возрастает - Х∈[0;+∞)
9. Вторая производная - Y"(x).
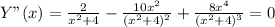
Корни производной - точки перегиба: х1 =-2√3/3, х3= 2√3/3. (≈1,15)
9. Выпуклая “горка» Х∈(-∞;-2√3/3)∪(2√3/3;+∞),
Вогнутая – «ложка» Х∈(-2√3/3;2√3/3).
10. Область значений Е(у) У∈(-∞;1)
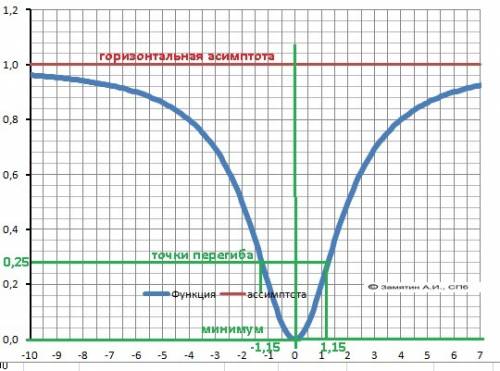
11. График в приложении
1) 567; 873; 882; 936; 468.
2) 120; 201; 351; 213; 405; 831; 219.
Пошаговое объяснение:
1) Числа, кратные числу 9, должны делиться на него без остатка.
К таким числам относятся, например: 9; 18; 27; 36 и т.д.
Признак делимости на 9: если сумма цифр числа делится на 9, то и число делится на 9.
*67; 6 + 7 = 13; 18 - 13 = 5; => искомое число: 567;
87*; 8 + 7 = 15; 18 - 15 = 3; => искомое число: 873;
8*2; 8 + 2 = 10; 18 - 10 = 8; => искомое число: 882;
9*6; 9 + 6 = 15; 18 - 15 = 3; => искомое число: 936;
46*; 4 + 6 = 10; 18 - 10 = 8; => искомое число: 468.
2) Числа, кратные 3, – это такие, которые без остатка делятся на 3.
К таким числам относятся, например: 3; 6; 9; 12; 15 и т.д.
Признак делимости на 3: целое число делится на 3, если сумма его цифр делится на 3.
1*0; 1 + 0 = 1; 3 - 1 = 2; => искомое число: 120;
2*1; 2 + 1 = 3; 3 - 3 = 0; => искомое число: 201;
35*; 3 + 5 = 8; 9 - 8 = 1; => искомое число: 351;
*13; 1 + 3 = 4; 6 - 4 = 2; => искомое число: 213;
4*5; 4 + 5 = 9; 9 - 9 = 0; => искомое число: 405;
83*; 8 + 3 = 11; 12 - 11 = 1; => искомое число: 831;
2*9; 2 + 9 = 11; 12 - 11 = 1; => искомое число: 219.