хє(-∞; 2)U((3+√5)/2; 3)
Пошаговое объяснение:
ОДЗ:
————————————————————
√(3-x)≠0
3-x≠0
x≠3
————————————————————
x-2≠0
x≠2
————————————————————
3-x≥0
x≤3
————————————————————
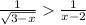
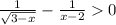
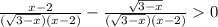
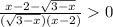
x-2-√(3-x)>0
x-2>√(3-x)
(x-2)²>√(3-x)²
x²+2²-2×x×2>3-x
x²+4-4x-3+x>0
x²-3x+1>0
D=b²-4ac=(-3)²-4×1×1=9-4=5
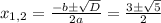
——————•————————•——————>х
x1 x2
х1=(3-√5)/2; х2=(3+√5)/2
100>x2
f(100)=100²-3×100+1=Положительное число
Ставим метки:
+ - +
——————•————————•——————>х
x1 x2
Функция больше нуля на промежутке:
(-∞; x1)U(x2; +∞)
У нас было ОДЗ:
x≠3x≠2x≤3хє(-∞; 2)U((3+√5)/2; 3)

Во-первых, у вас пропущено в самом первом условии, сколько времени работал второй.. .
Но я подозреваю, что там должно быть 4 часа :)
Подозреваю так я по двум причинам: с одной стороны – из-за слова часа 2,3,4 – c другими цифрами употребляется либо "час", либо "часов", с другой – из этих трёх значений только с четверкой задача имеет однозначное решение.
Из системы
2a+4b+6d=260
6b+6d+2c=270
b+d=40
(a,b,c,d – производительность в час, соответственно первого, второго )
получаем
a = 50-d
b = 40-d
c = 15
А нам нужно найти a+c+d = 50-d+15+d = 65
замена x^2=t
2t^4 -3t^3 -t^2 -3t+2=0
разделим на t^2
2t^2 -3t -1 -3/t +2/t^2 = 0
2(t^2 +1/t^2) -3(t+1/t) -1=0
сделаем замену
z= t+1/t
t^2 +1/t^2 = (t+1/t)^2 -2 =z^2 -2
2(z^2 -2) -3z -1=0
2z^2 -3z -5=0
D=9+4*5*2 = 49
z1=(3+7)/4 = 5/2
z2=(3-7)/4=-1
t+1/t = -1
t^2 +t+1=0
D<0 ==>> вещественных корней нет
t+1/t = 5/2
2t^2 -5t +2=0
D=25 -4*2*2 = 9
t1=(5+3)/4 = 2
t2=(5-3)/4 = 1/2
t^2 =2
t=+-sqrt(2)
t^2 =1/2
t=+- 1/sqrt(2)
этого получаются корни
x1=sqrt(2) ; x2=-sqrt(2) ; x3 = 1/sqrt(2) ; x4=-1/sqrt(2)
второе уравнение сам пробуй