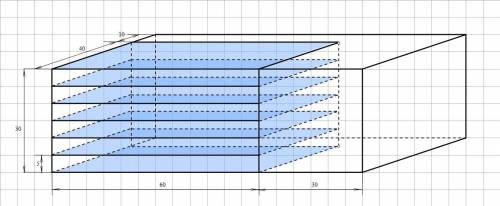
Объем начального бруска:
V₀ = abh = 30 · 50 · 90 = 135000 (см³)
Объем одной дощечки:
V₁ = a₁b₁h₁ = 5 · 40 · 60 = 12000 (см³)
Так как ширина и высота дощечки (40 и 60 см) меньше ширины и высоты бруска (50 и 90 см), а длина дощечки (5 см) укладывается в длине бруска (30 см) 6 раз, то от бруска возможно отпилить только 6 дощечек с указанными размерами. Причем, распилы можно производить только так, как показано на рисунке.
Общий объем дощечек:
V₆ = 6 · V₁ = 6 · 12000 = 72000 (см³)
Оставшийся брусок имеет угловую форму с объемом:
V = V₀ - V₆ = 135000 - 72000 = 63000 (см³)
Несмотря на то, что оставшийся объем бруска больше объема одной дощечки, ни одной дощечки с указанными размерами из бруска выпилить больше нельзя (если только имеются в виду целые, а не составные дощечки).
Если же остальные дощечки можно делать составными (с последующим склеиванием кусочков), то оставшегося объема бруска хватит еще на 5 дощечек:
N' = V : V₁ = 63000 : 12000 = 5 (ост. 3000)
Таким образом, из указанного бруска можно получить 6 целых и 5 составных дощечек с указанными размерами, причем объем остатка от бруска составит 3000 см³.
ответ: 6 целых и 5 составных дощечек.
Пошаговое объяснение:
Решим по формуле полной вероятности.
1) Вероятность мальчика - р(м) = 0,51.
Вероятность девочки - не мальчик: q(м) = 1 - р(м) = 0,49.
Событие повторяется ПЯТЬ раз и его ПОЛНАЯ вероятность по формуле:
2) Р5 = (p+q)⁵ = p⁵ + 5*p⁴q + 10*p³*q² + 10*p²*q³ + 5*p*q⁴ + q⁵ = 1.
В чём красота этой формулы - в неё описаны ВСЕ возможные варианты событий. Каждому члену выражение соответствует определенное событие.
Расчет и график к нему в приложении.
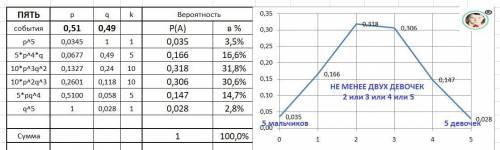
р⁵ = 0,035 - все пять детей мальчики.
q⁵ = 0.028 - все пять детей девочки.
5*p⁴*q = 0,166 - четыре мальчика и одна девочка .... и далее варианты.
ВНИМАНИЕ! ВАЖНО! ВНИМАНИЕ!
Описываем событие по условию задачи.
ВОПРОС: Вероятность НЕ МЕНЕЕ ДВУХ из ПЯТИ.
Это события ИЛИ - все 5 ИЛИ 4 ИЛИ 3 ИЛИ 2, но не одна или ни одной.
ВАЖНО! Вероятность событий ИЛИ равна сумме вероятностей каждого.
Р5(≥2) = q⁵ + 5*q⁴*p + 10*q³*p² + 10*q²*p³ =
0.028 + 0.147 + 0.306 + 0.319 = 0.80 - вероятность - ответ.
Решаем методом "от противного".
Q5(≥2) = p⁵ + 5*p⁴*q = 0.0345 + 0.1655 = 0.200 - меньше двух.
P5(≥2) = 1 - Q5(≥2) = 1 - 0.2 = 0.80 - ответ тот же.
Важно! Для расчета коэффициентов надо/можно использовать треугольник Паскаля - рисунок в приложении.