Пошаговое объяснение:
1)y= (√x+1 )+ 2/(x-4)
a) первое ограничение на √x - здесь х ≥ 0
б) второе ограничение на знаменатель (х-4) ≠ 0 - здесь х≠ 4
объединяем, получаем ООФ
{x ∈R: x ≥ 0; x≠4}
2)y= (√6-x) + 2/(x²-6x)
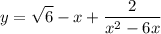
здесь ограничение только на знаменатель (x²-6x) = х(х-6)≠ 0
х ≠ 0 и х ≠ 6
{x ∈R: х ≠ 0; х ≠ 6}
3)y= (√x-2) - x+8/x-5
аналогично первому примеру ограничения на подкоренное выражение х ≥ 0 и на знаменатель (х-5) ≠ 0 ⇒ х ≠ 5
{x ∈R: x ≥ 0; x≠5}
примечание:
если бы скобки были расставлены иначе, например,
не так 1) y= (√x+1 )+ 2/(x-4)
а вот так 1)y= √(x+1 )+ 2/(x-4),
то область определения была бы другая
вот такая {x ∈R: x ≥ -1; x≠4}
Усеченый конус АВСД, О -центр нижнего основания, О1 центр верхнего основания, АО=ВО=радиус нижнего основания=корень(площадь/пи)=корень(пи/пи)=1, АВ-диаметр нижнего основания=2*1=2, ВС-диаметр верхнего основания, ВО1=СО1=радиус верхнего основания=корень(площадь/пи)=корень(16пи/пи)=4, ВС=2*4=8, АВ=СД=5-образующая, сечение-равнобокая трапеция АВСД, АВ=СД, уголА=уголД, проводим высоты ВН и СК на АД, ВН=СК, треугольник АВН=треугольник КСД как прямоугольные по гипотенузе и острому углу, АН=КД, НВСК прямоугольник ВС=НК=2, АН=КД=(АД-НК)/2=(8-2)/2=3, треугольник АВН прямоугольный, ВН -высота трапеции=корень(АВ в квадрате-АН в квадрате)=корень((25-9)=4, площадь АВСД (сечения)=(АД+ВС)*ВН/2=(2+8)*4/2=20
Пошаговое объяснение:
я не уверена что это правильно но посмотри и не пиши мне плохие коментарии
x=3/4-1/8
x=5/8
Проверка: 5/8+1/8=6/8=3/4