Пошаговое объяснение:
|1+2x|<9
Допустим: |1+2x|=9
При 1+2x≥0:
1+2x=9; x₁=(9-1)/2=4
При 1+2x<0:
-1-2x=9; -2x=9+1; x₂=10/(-2)=-5
Проверка при x₁>4; x₂>-5: |1+2·5|<9; |11|<9; 11>9 - неравенство не выполняется.
Проверка при x₁<4; x₂<-5: |1+2·(-6)|<9; |-11|<9; 11>9 - неравенство не выполняется.
Проверка при x₁<4; x₂>-5: |1+2·0|<9; |1|<9 - неравенство выполняется.
Проверка при x₁>4; x₂<-5: |1+2·5|<9; |11|<9; 11>9 - неравенство не выполняется; |1+2·(-6)|<9; |-11|<9; 11>9 - неравенство не выполняется.
Следовательно: -5<x<4
ответ: x∈(-5; 4)
а) -(29/140)
б) 71/140
Пошаговое объяснение: Сначала надо найти наменьший общий знаменатель, для этого нужно найти их найменьшее общее кратное, то есть число на которое бы они оба делились без остатка, в данном случае этим числом будет 140, т.к. делиться без остатка на 20 получается 7, и делиться без остатка на 14 получается 10. Теперь нужно домножить каждую дробь на такое число, чтобы получалось в знаменателе 140, у 14 это 10, а у 20 это 7, ну и умножаешь каждую дробь на свои множители, то есть на 7 и на 10, при чем умножаешь и числитель и знаменатель и получаешь равносильную дробь(основное свойство дроби). Ну а потом просто складываешь числители, а знаменатель остаётся 140
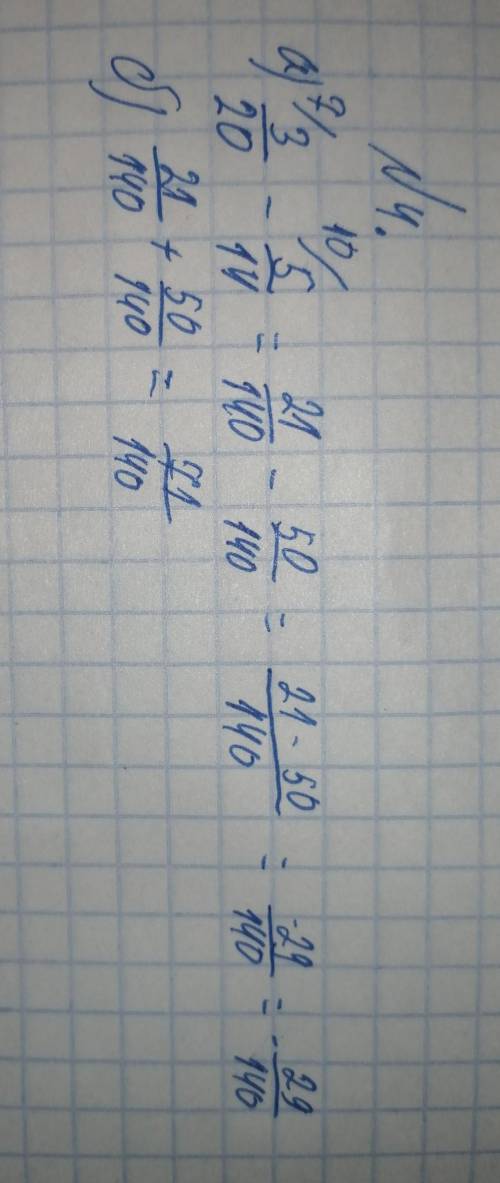
4*(x-2)=3*(2x+3), 4 и 3 дополнительные множители
раскрываем скобки: 4x-8=6x+9, 4x-6x=9+8, -2x=17, x=-8,5
в)Исходя из условия получаем, что 2-е выражение больше 1-го на 2, следовательно получается уравнение 3/4-5/6*z-(1/2*z-2/3)=2.
Раскрывая скобки получаем : 3/4-5/6*z-1/2*z+2/3=2, приводим к общему знаменателю: 12.
Умножаем каждый член уравнения на 12:
3/4*12-5/6*12*z-1/2*z*12+2/3*12=24
9--10z-6z+8=24
-16z+17=24
-16z=24-17
-16z=7
z=-7/16
б) 17-5у=-(17у+19)
Раскрываем скобки: 17-5у=-17у-19, -5у+17у=-19-17, 12у=-36, у= -36/12=-3
г) (2,6р-9,8)/р=4, умножаем обе части выражения на р≠0
2,6р-9,8=4р
2,6р-4р=9,8
-1,4р= 9,8
р=9,8/(-1,4)
р=-7