Пошаговое объяснение:
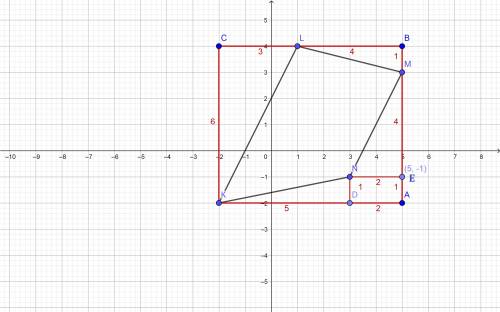
рисунок во вложении
Построим прямоугольник KCBA
проходящий через вершины K,L,M четырехугольника KLMN
Найдем площадь получившегося прямоугольника
S прям KCBA=a*b
S=6*7=42 cм²
Теперь найдем площади прямоугольных треугольников
KCL, LBM. MEN ,KDN и прямоугольника DNEA
Формула площади прямоугольного треугольника
S=1/2 a*b, где a и b катеты

Теперь вычтем все площади треугольников и прямоугольника DNEA из площади прямоугольника KCBA и получим площадь четырехугольника KLMN
S=42-9-2-4-2,5-2=22,5 см²
ответ: площадь четырехугольника KLMN составляет 22,5 см²
P.S. Я надеюсь, что вы все это уже изучали
P = (a + b) · 2
p = a + b = 24
Варианты длины и ширины:
a₁ = 23, b₁ = 1 a₂ = 22, b₂ = 2 a₃ = 21, b₃ = 3
a₄ = 20, b₄ = 4 a₅ = 19, b₅ = 5 a₆ = 18, b₆ = 6
a₇ = 17, b₇ = 7 a₈ = 16, b₈ = 8 a₉ = 15, b₉ = 9
a₁₀ = 14, b₁₀ = 10 a₁₁ = 13, b₁₁ = 11
Вариант 12 и 12 уже не подходит, у нас прямоугольник, а не квадрат.
S₁ = 23 · 1 = 23 см² S₂ = 22 · 2 = 44 см² S₃ = 21 · 3 = 63 см²
S₄ = 20 · 4 = 80 см² S₅ = 19 · 5 = 95 см² S₆ = 18 · 6 = 108 см²
S₇ = 17 · 7 = 119 см² S₈ = 16 · 8 = 128 см² S₉ = 15 · 9 = 135 см²
S₁₀ = 14 · 10 = 140 см² S₁₁ = 11 · 13 = 143 см²
х²-8х+15=0
Используем теорему Виета
х1+х2=8 х1*х2=15
х1=3,х2=5.
х²-8х+15=(х-3)(х-5)
(х²-8х+15)/(х-3)=(х-3)(х-5)/(х-3)=х-5