Из 1000 новорожденных 511 оказались мальчиками. Найдите вероятность рождения мальчика и вероятность рождения девочки
Задачка на простейшую теорию вероятности. Решать будем по следующей формуле:
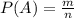, где m - количество удовлетворяющих нам вариантов события, а n - количество всех вариантов этого события.
Тогда, так как 511 детей - мальчики, а всего родившихся 1000, найдем вероятность рождения мальчика:
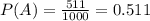
Найдем сколько родилось девочек:
1000 - 511 = 489
Тогда, по алгоритму нахождения вероятности рождения мальчика, найдем вероятность рождения девочки:
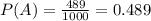
ответ: 0.489 - вероятность рождения девочки; 0.511 - вероятность рождения мальчика.
Будем применять неравенство треугольника для исключения невозможных случаев. Если длина диагонали равна 7, 5, то оставшиеся четыре числа можно разбить на две пары так, что сумма чисел в каждой из них больше 7, 5. Но этого, очевидно, сделать нельзя. Аналогично, не подходит 5. Если длина диагонали равна 1, то оставшиеся четыре числа можно разбить на две пары так, что разность чисел в каждой из них меньше 1, но этого, очевидно, сделать нельзя. Аналогично, не подходит 2.
Остаётся единственный вариант — 2, 8. Четырёхугольник по условию существует. Поэтому, доказывать, что 2, 8 на самом деле подходит, не обязательно (хотя и полезно, чтобы проверить своё решение или даже найти ошибку в условии!)
5х = 4;
х = 0,8.