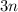- где n число. Подставим к примеру три натуральных числа вместо n. И получим нужные нам числа:
- где m число. Подставим к примеру три натуральных числа вместо m. И получим нужные нам числа: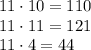
ответ: x=-3.
Пошаговое объяснение:
Данная функция определена и непрерывна на всей числовой оси. Находим её производную: y'=2*(x+3)*(x-2)+(x+3)²=3*x²+8*x-3. Приравнивая её к нулю, получаем квадратное уравнение 3*x²+8*x-3=0, которое имеет решения x1=1/3 и x2=-3. Значит, функция имеет две критические точки: x1=1/3 и x2=-3. Если x<3, то y'>0, поэтому на интервале (-∞;-3) функция возрастает. Если -3<x<1/3, то y'<0, так что на интервале (-3;1/3) функция убывает. Наконец, если x>1/3, то y'>0, поэтому на интервале (1/3;∞) функция возрастает. Значит, точка x=-3 является точкой максимума, а точка x=1/3 - точкой минимума.
ответ:
пошаговое объяснение:
-3 1\2: (-1 2\3-3 1\12) и 5\18*(-1 5\7)+1 3\14
-3 1\2: (-1 2\3-3 1\12)= -7/2: (-5/3-37/12)=-7/2: (-20/12-37/12)=-7/2: (-57/12)=
=-7/2*(-12/57)=42/57
5\18*(-1 5\7)+1 3\14=5/18*(-12/7)+17/14=-10/21+17/14= -40/84+102/84=
=62/84=31/42
42/57 меньше 31/42