за 7 часов тракторист вспахал 4,9 га. с какой скоростью двигался трактор, если ширина полосы, вспахиваемая плугами равна 1,75 метров?
решение
к одной размерности: 1 га = 100*100м=1*10^4м^2
v=4.9/7=0.7 га/час=0,7*10^4=7000м^2/час
для удобства расчетов примем:
7000м^2=а*1,75 а=7000/1,75=4000 м т.е. мы приняли, что 7000 м^2 равны длине поля 4000 метров при ширине поля 1,75 м (т.е. ширине полосы плуга). тогда: v=7000м^2/час=1,75м*4000м/час=4000 м/час или 4 км/час
ответ: скорость движения трактора равна 4 км/час
при
0+ = -∞
0- = ∞
Пошаговое объяснение:
В данном решении будем пользоваться правилом произведения пределов и выделим функции
f(x) = 9x - 9
g(x) = 1/10 * x
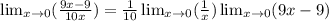
далее вычислим самый правый предел в 0, т. к. он точно существует
9 * 0 - 9 = -9
теперь наше выражение выглядит так:
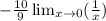
у 1/x есть асимптота y = 0 и предела двустороннего предела в 0 не существует
тогда вычислим пределы слева и справа
Пусть существует точка M > 0 и δ = 1/M тогда:
для 0+ имеем выражение 1/x > 1/(1/M) = M для всех 0 < x < δ
для 0- имеем выражение -1/x > 1/(1/M) = -M для всех -δ < x < 0
откуда получаем:
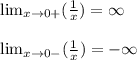
теперь полученные значения подставим в основное выражение:
-9/10 * (-∞) = ∞
-9/10 * ∞ = -∞