Во 2-ой коробке изначально было 40 карандашей.
Пошаговое объяснение:
Пусть в 1-ой коробке - а карандашей,
во 2-ой коробке - b карандашей, а
в 3-ьей коробке - с карандашей.
Когда из 1-ой коробки взяли 6 кар.,
в ней осталось (а-6) карандашей.
Когда из 2-ой коробки взяли (а-6) кар., в ней осталось b-(а-6) каранд.
По условию карандашей в 3-х коробках после этого стало поровну,
следовательно:
а-6=b-(a-6)=c, отсюда получаем
с=а-6 ( кол-во каранд. в 3-ей кор.)
b=a-6+a-6=2a-12 (кол-во. карандашей во 2-ой коробке).
По условию всего в 3-х коробках было 86 карандашей, следоват-но:
а+2a-12+a-6=86
4a=104
a=104:4
a=26 (карандашей в 1-ой коробке).
b=2*26-12=52-12=40 (кар.во 2-ой кор.)
с=26-6=20 (карандашей в 3-ьей кор.).
ответ: изначально во 2-ой коробке было 40 карандашей.
Проверка: а+b+c=86
26+40+20=86
86=86
√3
Пошаговое объяснение:
Не теряя общности, положим AD ≤ AB. Опустим перпендикуляры CK и CM на стороны угла. Обозначим AD = x, DK = y.
Так как AC — биссектриса, точка C равноудалена от сторон угла, то есть CK = CM. Прямоугольные треугольники AKC и AMC равны по катету (CK = CM) и гипотенузе (AC — общая) ⇒ AK = AM = x + y.
Так как ∠DAC = ∠BAC, DC = BC как хорды, на которые опираются равные углы. Прямоугольные треугольники DKC и BMC равны по катету (CK = CM) и гипотенузе (DC = BC) ⇒ DK = BM = y.
По условию AB + AD = (x + y + y) + x = 2(x + y) = 2 ⇒ x + y = 1. Тогда AM = x + y = 1. В прямоугольном треугольнике AMC ∠ACM = 90° - ∠CAM = 90° - 60° = 30°. По теореме об угле в 30° AC = 2AM = 2.
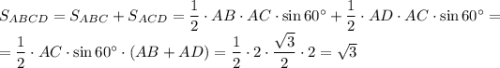
1200 х 3 : 6 = 600 м2 - засеяно капустой