 . Перемножаем крест-накрест и получаем x = 700 – искомое число.
. Перемножаем крест-накрест и получаем x = 700 – искомое число. 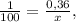

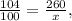
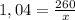
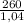 =
= 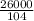
В решении.
Пошаговое объяснение:
1294.
Решить систему уравнений:
1.
х + у = 4/3
3х - 2у = -1
Умножить все части первого уравнения на 3, чтобы избавиться от дробного выражения:
3х + 3у = 4
3х - 2у = -1
Умножить первое уравнение на -1, чтобы решить систему сложением:
-3х - 3у = -4
3х - 2у = -1
Сложить уравнения:
-3х + 3х - 3у - 2у = -4 - 1
-5у = -5
у = -5/-5 (деление)
у = 1;
Теперь подставить значение у в любое их двух данных уравнений и вычислить х:
3х - 2у = -1
3х = -1 + 2у
3х = -1 + 2*1
3х = -1 + 2
3х = 1
х = 1/3 (дробь);
Решение системы уравнений: (1/3; 1);
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
2.
5х + у = 1/6
х - 2у = -2 1/6
↓
5х + у = 1/6
х - 2у = -13/6
Умножить оба уравнения на 6, чтобы избавиться от дробного выражения:
30х + 6у = 1
6х - 12у = -13
Умножить второе уравнение на -5, чтобы решить систему сложением:
30х + 6у = 1
-30х + 60у = 65
Сложить уравнения:
30х - 30х + 6у + 60у = 1 + 65
66у = 66
у = 66/66
у = 1;
Теперь подставить значение у в любое их двух данных уравнений и вычислить х:
5х + у = 1/6
5х = 1/6 - у
5х = -5/6
х = -5/6 : 5
х = -1/6 (дробь);
Решение системы уравнений: (-1/6; 1);
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
3.
у + 2х = -1
5х - 4у = 10,5
Выразить у через х в первом уравнении, подставить выражение во второе уравнение и вычислить х:
у = -1 - 2х
5х - 4(-1 - 2х) = 10,5
5х + 4 + 8х = 10,5
13х = 10,5 - 4
13х = 6,5
х = 6,5/13 (деление)
х = 0,5;
Теперь вычислить у:
у = -1 - 2х
у = -1 - 2*0,5
у = -1 - 1
у = -2;
Решение системы уравнений: (0,5; -2);
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
В решении.
Пошаговое объяснение:
Задача 1.
Аквариум имеет форму куба со стороной 50 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.
V = а³;
V = 50³ = 125 000 (cм³)
125 000 : 1000 = 125 (л).
Задача 2.
Площадь грани куба равна 25 см². Найти объём куба.
1) S = а² → а = √S → а = √25 → а = 5 (см);
2) V = а³ → V = 5³ → V = 125 (см³).
Задача 3.
Ребро куба равно 10 см. Найти объём куба.
V = a³ → V = 10³ → V = 1000 (см³).
Задача 4.
Объём куба равен 27 см³. Найти длину его ребра.
V = a³ → а = ∛V → a = ∛27 → а = 3 (см).
Задача 5.
Даны два прямоугольных параллелепипеда: ребра одного равны 18 см, 15 см и 7 см; а ребра другого равны 18 см, 5 см и 7 см. Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда?
V = a * b * c;
V₁ = 18 * 15 * 7 = 1890 (см³);
V₂ = 18 * 5 * 7 = 630 (см³);
V₁ : V₂ = 1890 : 630 = 3 (раза).
Задача 6.
Дан прямоугольный параллелепипед с площадью основания 48 см² и высотой 10 см. Найти объём параллелепипеда.
V = S * h → V = 48 * 10 = 480 (см³).
Задача 7.
Объём прямоугольного параллелепипеда 225 см³. Его длина - 15 см, ширина - 10 см. Найти высоту параллелепипеда.
1) 15 * 10 = 150 (см²) - площадь основания;
2) 225 : 150 = 1,5 (см) - высота параллелепипеда.
Задача 8.
Длина параллелепипеда - 20 см, ширина в два раза меньше, а высота в два раза больше длины. Найти объём параллелепипеда.
1) 20 : 2 = 10 (см) - ширина;
2) 20 * 2 = 40 (см) - высота;
3) V = a*b*c → 20 * 10 * 40 = 8000 (см³) - объём.
2)во втором - 36;
3)в третьем - 40;
4) в четвертом - 450.
Объяснить как я это получила?