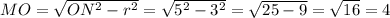1) Площадь основания (ромба) So = a²sin 60° = 36*√3/2 = 18√3 см².
Проекция высоты боковой грани на основание - это половина высоты h основания: (h/2) = asin 60°/2 = 6*√3/(2*2) = 3√3/2 см.
Так как угол наклона боковой грани к основанию равен 45 градусов, то высота H пирамиды равна (h/2).
Отсюда находим объём пирамиды:
V = (1/3)SoH = (1/3)*(18√3)*(3√3/2) = 27 см³.
2) Проекция бокового ребра на основание равна стороне основания.
Площадь основания равна: So = a²3√3/2 = 1*3√3/2 = 3√3/2.
Объём пирамиды V = (1/3)SoH. Отсюда находим высоту пирамиды: Н = 3V/So = 3*6/(3√3/2) = 4√3.
Тогда боковое ребро L = 4√3*√2 = 4√6.
ответ: 4 .
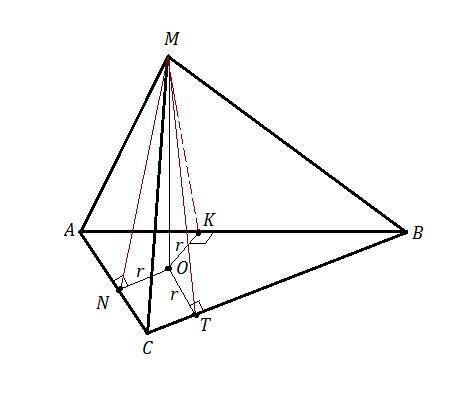
ΔАВС , d(М,АВ)=d(М,ВС)=d(М,АС)=5 , АС=9 , ВС=12 , М∉АВС , ∠С=90°
Найти d(M,ABC) .
По теореме Пифагора: АВ=√(АС²+²ВС²)=√(9²+12²)=√225=15 .
MN⊥AC , MT⊥BC , MK⊥AB ⇒ d(М,АВ)=MK , d(М,ВС)=MT , d(М,АС)=MN .
MK=MT=MN=5 .
Так как расстояние от точки М до сторон треугольника одинаковое, то точка М проектируется на плоскость треугольника АВС в центр вписанной окружности О . d(M,ABC)=MO .
MO⊥ABC , ON=OT=OK= r (радиусу вписанной окружности) .
∠MON=∠MOT=∠MOK=90° , ΔMNO=ΔMTO=ΔMNO (по катету и гипотенузе)

По теореме Пифагора имеем: