В жизни часто приходится встречаться с различными совокупностями объектов, объединёнными в одно целое по некоторому признаку. Для обозначения этих совокупностей используются различные слова. Например, говорят: «стадо коров», «букет цветов», «команда футболистов» и т. д.
В математике в целях единообразия для обозначения совокупностей употребляется единый термин — множество. Например, говорят: множество чётных чисел, множество двузначных чисел, множество правильных дробей со знаменателем 5.
Термин «множество» употребляется и тогда, когда речь идёт о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек координатной плоскости, о множестве прямых, проходящих через данную точку.
Объекты или предметы, составляющие множество, называют элементами множества. Например, число 89 — элемент мнoжества двузначных чисел; точка В — элемент мнoжества вершин многоугольника ABCDE.
Множeства бывают конечные и бесконечные. Например, множество двузначных чисел — конечное множество (оно содержит 90 элементов), а множество чётных чисел — бесконечное множество.
Пошаговое объяснение:
в 5 раз дыня тяжелее корнеплода свеклы.
Пошаговое объяснение:
Пусть х кг - масса арбуза,
у кг - масса дыни,
z кг - масса кочана капусты,
t кг - масса корнеплода свеклы.
Так как масса дыни и корнеплода свеклы совпадает с массой арбуза.
y+t=x. (1)
Общая масса кочана капусты и корнеплода свеклы равна массе дыни
z+t=y. (2)
Два арбуза имеют такую же массу, как три кочана капусты
2х=3z. (3)
Нам нужно узнать 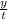 .
.
Из второго уравнения выразим z через t и у.
z=y-t (2°). Из первого же уравнения получаем х=y+t (1°). Теперь подставим х и z, выраженные через у и t, в уравнение (3).
Получаем 2(y+t)=3(y-t).
2y+2t=3y-3t
2t=3y-3t-2y
2t=3y-2y-3t
2t=y-3t
2t+3t=y
y=5t.
То есть масса дыни у весит в 5 раз больше корнеплода свеклы t.
Получается, что 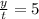 .
.