17
Пошаговое объяснение:
Объём пирамиды:
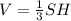 , где Н -высота пирамиды, S- площадь основания.
, где Н -высота пирамиды, S- площадь основания.
Высота пирамиды, половина диагонали основания - как катеты и боковое ребро - как гипотенуза образуют прямоугольный треугольник.
Обозначим половину диагонали как а, тогда квадрат бокового ребра равен:
Н²+а².
Найдем а.
Т.к. пирамида - правильная, то в основании лежит квадрат. Значит его сторона равна √16=4. А диагональ такого квадрата равна: √(4²+4²)=√32.
Значит а=√32/2
Найдем Н из формулы объёма пирамиды.
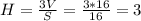
Тогда квадрат бокового ребра равен:
Н²+а² = 3² + 32/4 = 9+8 = 17.
x--- 100%
7---30%
1) х/7=100/30
х × 30=100 × 7
30х = 700
х= 700÷30
х= 23,3 (см) длинна
2) 23,3×7= 161,1(см в квадрате) площадь
вроде так