1) а) 16 б) -0,5 в) -2 г) 6 д) 0 е) Решений нет ж) 0 з) -5
2) а) -4 б) -1 в) -2 г) -6 д) 0 е) Решений нет ж) 0 з) 6,4
Объяснение:
1) а) 2х-5=27
2х=32
х=16
б) -3+4у=-5
4у=-2
у=-0,5
в) 2х-1=4х+3
2х=-4
х=-2
г) 1/3у+2=-1/6у+5
1/3у+1/6у=3
3/6у=3
0,5у=3
у=6
д) 2х-(5х-6)=7+(х-1)
-3х+6=6+х
-4х=0
х=0
е) 3х-1=2х-(4-х)
3х-1=3х-4
3х-3х=-3
0х=-3?
Решений нет
ж) 2(х-3)=-3(х+2)
2х-6=-3х-6
5х=0
х=0
з) 2(х-5)-7(х+2)=1
2х-10-7х-14=1
-5х=25
х=-5
2) а) 4-3х=16
-3х=12
х=-4
б) 5у-7=-12
5у=-5
у=-1
в) 7х-1=2х-11
5х=-10
х=-2
г) 1/2у-3=-1/6у-7
4/6у=-4
у=-4/(4/6)
у=-6
д) 5х-(2х-9)=6+(х+3)
3х+9=9+х
2х=0
х=0
е) 7х-8=4х-(1-3х)
7х-8=7х-1
7х-7х=7
0х=7
Решений нет
ж) 3(х+4)=-4(х-3)
3х+12=-4х+12
7х=0
х=0
з) 3(х+2)-8(х-4)=-2
3х+6-8х+24=-2
-5х=-32
х=6,4
а) -20 = -5 + (-15);
б) -20 = -14,6 + (-5,4);
в) 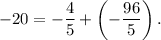
Объяснение:
Требуется представить число (-20) в виде суммы двух отрицательных слагаемых, учитывая заданные условия.
Вспомним правило сложения чисел одного знака:
чтобы сложить два числа одинаковых знаков, нужно сложить их модули и поставить перед суммой знак слагаемых.
а) Оба слагаемых целые числа.
Представим число (-20) в виде суммы двух целых отрицательных чисел, например, так:
-5 + (-15) = -(5+15) = -20.
б) Оба слагаемых десятичные дроби.
Представим число (-20) в виде суммы двух отрицательных десятичных дробей, например, так:
-14,6 + (-5,4) = -(14,6 + 5,4) = -20.
б) Одно из слагаемых правильная дробь.
Положительная дробь называется правильной, если ее числитель меньше знаменателя. Если перед положительной дробью поставить знак минус, то получится отрицательная дробь.
Например, так представим число (-20) в виде суммы двух отрицательных дробей, одна из которых правильная.
Число (-20) представим в виде дроби со знаменателем 5, а потом полученную дробь представим как сумму двух дробей (не забудем, что одна из них должна быть правильной):