Числа A и B называются взаимно простыми, если НОД(А; В)=1.
Возможны различные варианты :
а) Если числа А и В простые, то НОД(А; В)=1. Например:
НОД(2; 3)=1, НОД(2; 5)=1, НОД(3; 7)=1.
1) 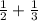
Так как НОД(2; 3)=1, то НОК(2; 3)=2·3=6
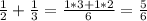
2) 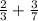
НОД(3; 7)=1, то НОК(3; 7)=3·7=21
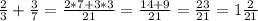
б) Если числа А и В составные, но не имеют одинаковых простых делителей, тогда НОД(А; В)=1. Например:
НОД(4; 9)=1, НОД(4; 25)=1, НОД(9; 16)=1.
3) 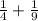
Так как НОД(4; 9)=1, то НОК(4; 9)=4·9=36
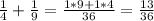
2) 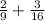
НОД(9; 16)=1, то НОК(9; 16)=9·16=144
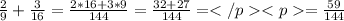
В общем случае, если А и В взаимно простые, то есть
НОД(А; В)=1, то НОК(А; В)=А·В.
5х-700
Но, цена куртки дороже стоимости двух шапок на 200 рублей, что позволяет составить вторую часть равенства 2х+200
Решаем уравнение:
5х-700=2х+200
5х-2х=200+700
3х=900
х=900÷3
х=300
5×300-700=2×300+200
1500-700=600+200
800=800
800руб. стоит куртка
ответ:
300 рублей стоит шапка