Сначала идет цифры 400401402403... Разделим их по 3: 400.401.402.403... Теперь стираем по 3 цифры, то есть по одному трёхзначному числу. Стерли 101 раз по 3 цифры, то есть до 500, получили: 501.502.503.504... Это мы стерли 303 цифр, и надо стереть еще 200 цифр. Стираем 180 = 3*60 цифр, то есть числа от 501 до 560. Получили: 561.562.563.564... Стираем еще 18 цифр, то есть 6 чисел, от 561 до 566. Осталось: 567.568.569.600... И осталось стереть 2 цифры, 5 и 6. Всего мы стерли 303+180+18+2=503 цифры, как и хотели. Осталась первая цифра 7.
Пошаговое объяснение:
сначала упростим общий вид членов ряда
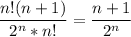
(это можно сделать, пользуясь свойствами пределов - получим равнозначный ряд)
теперь применим ризнак Даламбера
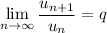
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - неопределенность (дополнительные исследования)
у нас
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования)
у нас
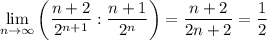
q < 1 - ряд сходится
( можно было и сразу "в лоб" применять признак Даламбера не упрощая формулу - результат был бы тот же...)