190 прямых
Пошаговое объяснение:
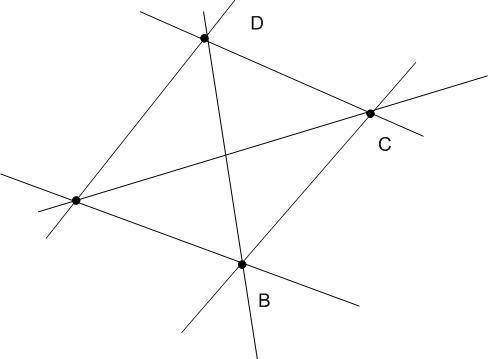
попробуем построить, ну, например для 4-х точек (см.рис).
Прямая проходит через каждые две точки. Т.е. нужно посчитать сколько различных пар точек можно выбрать из 4-х точек. Это - известная в комбинаторике формула для подсчета числа сочетаний (именно сочетаний, а не размещений, потому, что прямая АВ и прямая ВА - одна и таже прямая). Подсчитаем для 4-х точек:
C₄²=4!/(4-2)!4!=4!/(2!*2!)=3*4/2=6;
и действительно видим 6 прямых. Тогда для 20 точек:
C₂₀²=20!/((20-2)!2!)=19*20/2=190.
(3/4 + 1/6) * 3 + (5/6 - 1/2) : 2/9
По действиям
34 + 1/6 = 11/12
11/12 *3 = 2 3/4 - слагаемое
5/6 - 1/2 = 1/3
1/3 : 2/9 = 1 1/2 - слагаемое
2 3/4 + 1 1/2 = 4 1/4 - ОТВЕТ