Если сделать рисунок, получается в окружность вписан четырехугольник PKBC.
Для вписанного четырехугольника необходимо выполнение условия - сумма противолежащих углов д.б. равна 180. Значит, сумма углов PKB и PCB равна 180.
Но сумма углов PKB и AKP также равна 180 (т.к. угол AKB развернутый). Т.о. получается, что угол AKP равен углу PCB в тр-ках AKP и ACB соответственно, а угол А у ни общий. Значит, тр-к АКР подовен тр-ку АСВ по 2-м углам.
Далее
АК / АС = КР / ВС
6 / (1,5*ВС) = КР / ВС умножим обе части на ВС
6 / 1,5 = КР
КР = 4
Диагонали трапеции равны 13 и корень из 41, а высота равна 5.
Найдите площадь трапеции
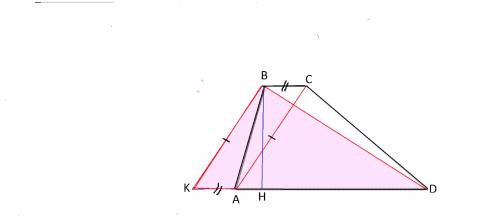
Сделаем рисунок к задаче.
Из вершины В проведем прямую ВК параллельно диагонали АС, равной √ 41, к продолжению стороны AD до пересечения с ней.
Рассмотрим четырехугольник АСВК.
В нем стороны попарно параллельны, и потому это - параллелограмм. АК=ВС.
Отсюда КD=AD+BC, т.е сумме оснований трапеции.
Следовательно, площадь треугольника КВD равна площади трапеции - т.е. произведению высотыВН на половину КD.
КD=KH+HD
КН²=ВК²-ВН²=41-25=16
КН=√16=4
HD²=BD²-BH²=169-25=144
HD=√144=12
AD=12+4=16
S ABD=S ABCD=KD*BH:2=16*5:2=40
(a^2-b^2)=(a-b)(a+b)
Следуя этой формуле, мы получаем:
(2√13-1)(2√13+1)=((2√13)^2-(1)^2)=(52-1)