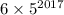Современное значение понятия экология имеет более широкое значение, чем в первые десятилетия развития этой науки. В настоящее время чаще всего под экологическими вопросами ошибочно понимаются, прежде всего, вопросы охраны окружающей среды. Во многом такое смещение смысла произошло благодаря всё более ощутимым последствиям влияния человека на окружающую среду, однако необходимо разделять понятия ecological («относящееся к науке экологии») и environmental («относящееся к окружающей среде»). Всеобщее внимание к экологии повлекло за собой расширение первоначально довольно чётко обозначенной Эрнстом Геккелем области знаний (исключительно биологических) на другие естественные, а также гуманитарные науки.
Образное описание экологии: наука, изучающая взаимоотношения живой и неживой природы.[2]
Другое определение (экология — биологическая наука, которая исследует структуру и функционирование систем надорганизменного уровня (популяции, сообщества, экосистемы) в пространстве и времени в естественных и измененных человеком условиях) дано на 5-м Международном экологическом конгрессе (1990) с целью противодействия размыванию понятия экологии, наблюдаемому в настоящее время. Однако это определение полностью исключает из компетенции экологии как науки аутэкологию (см. ниже), что в корне неверно[3].
Пусть мы красим в белый и черные цвета. Заметим, что в любой правильной раскраске должно быть поровну обоих цветов. Иначе в каком-нибудь квадрате 2x2 найдется три клетки одного цвета, что невозможно. Теперь будем по порядку рассматривать квадраты 2x2. Пусть изначально прямоугольника покрашен в шахматную расцветку. Для того, чтобы получать новую раскраску будем двигать черные (без ограничения общности - двигая черные мы, грубо говоря, двигаем и белые) клетки (в квадратах, двигаясь слева направо), причем так, чтобы не возникало уголков. Действительно, если они будут возникать, то их придется устранять и тем самым создавать их в квадратах, расположенных правее и в конце концов упремся. Таким образом, для первого квадрата существует три движения (включая тождественную перестановку). Для второго квадрата существует два варианта - если мы двигали черную клетку, стоящую в пересечении первого и второго квадратов, то движений 2, если нет - то три. Итак, можно построить дерево (см. рис.). При переходе по стрелке мы умножаем числа, стоящие в вершинах. В конце концов, числа до которых нельзя добраться, складываем. Итог - кол-во Докажем по индукции, что искомое количество равно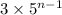 , где n - номер уровня (ступени).
, где n - номер уровня (ступени).
База очевидна: при n=1 результат 3, что верно.
Переход: пусть для некоторого n=k верно. Докажем, что верно и для n=k+1. Рассмотрим k+1-ый уровень. Количество троек равно количеству двоек. Поэтому каждое слагаемое, входящее в сумму, которая равна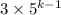 можно умножить сначала на тройки, а потом на двойки, что равнозначно
можно умножить сначала на тройки, а потом на двойки, что равнозначно 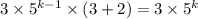 , переход доказан.
, переход доказан.
Не забудем итоговый ответ также домножить на два, так как существует две различные шахматные расцветки прямоугольника.
Имеем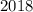 квадратов, а, стало быть, уровней.
квадратов, а, стало быть, уровней. 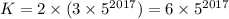 ;
;
ответ: