Рассмотрим случай разрезания стола по диагонали. Пусть стол представляет собой некоторый n-угольник.
1) Количество диагоналей многоугольника, проведенных из одной вершины = n-3;
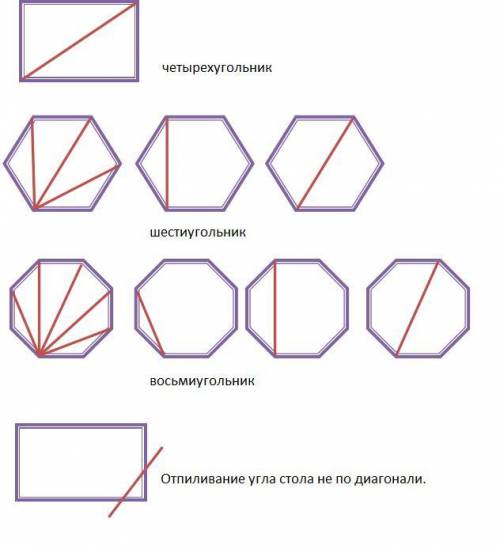
Например, у четырехугольника (n=4) 1 диагональ, у шестиугольника (n=6) 3 диагонали, у восьмиугольника (n=8) 5 диагоналей, проведенных из одной вершины.
2) При разрезании n-угольника по любой из них получаем две фигуры с общим количеством вершин = n+2.
Например.
При разрезании четырехугольника по диагонали получим 2 треугольника. Всего вершин у полученных фигур = 6; 6 = 3+3.
При разрезании шестиугольника по любой диагонали получим 2 фигуры с общим количеством вершин = 8, 8 = 3+5 = 4+4 (треугольник и пятиугольник или два четырехугольника).
При разрезании восьмиугольника по любой диагонали получим 2 фигуры с общим количеством вершин = 10; 10 = 3 + 7 = 4 + 6 = 5+5.
3) Т.о. при разрезании многоугольника по одной диагонали, получим фигуру с меньшим числом вершин, чем у исходного многоугольника на величину от 1 до n-3, т.е. получим многоугольники с количеством вершин = 3, 4, 5…, n-1.
При разрезании угла стола не по диагонали: количество углов у большей части стола увеличится на 1 по сравнению с исходным многоугольником.
Методом подбора рассмотрим крайние варианты:
1 вариант
Мальчики сбивали кегли 13 раз. За эти 13 раз Юра не сбил ни одной, а так как Антон каждый раз сбивал больше, чем Юра, то выглядеть это может так:
Юра Антон
0 1
0 1
0 1
0 1
0 1
0 1
0 1
0 1
0 1
0 1
0 1
0 1
0 1
Итого: Юра сбил 0 кеглей, Антон сбил 13 кеглей
2 вариант
Пусть Юра сбил сразу 6 кеглей. Тогда Антон сбил 7 кеглей
Как мы видим, вариантов может быть несколько:
Юра сбил 0 кеглей, Антон - 13 кеглей
Юра сбил 1 кеглю, Антон - 12 кеглей
Юра сбил 2 кегли, Антон - 11 кеглей
Юра сбил 3 кегли, Антон - 10 кеглей
Юра сбил 4 кегли, Антон - 9 кеглей
Юра сбил 5 кеглей, Антон - 8 кеглей
Юра сбил 6 кеглей, Антон - 7 кеглей