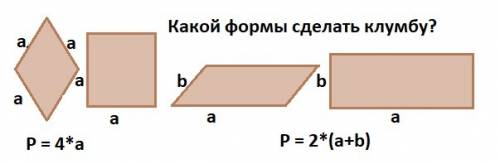
В задаче не сказано какой формы будут клумбы - вот и задумался садовник. Рисунок к задаче в приложении.
Если стороны равны - а , то это ромб или квадрат. Тогда периметр по формуле: Р = 4*а.
Если стороны разные: a и b, то это параллелограмм или прямоугольник и периметр по формуле: P = 2*(a + b).
1) а = b = 4 м. Р1 = 4*а = 4*4 = 16 м - периметр первой клумбы.
2) Р2 = 2*(6 + 4) = 2*10 = 20 м - периметр второй клумбы
3) Р3 = 2*(7 + 2) = 2*9 = 18 м - периметр третьей клумбы.
4) Р4 = 2*(5 + 3) = 2*8 = 16 м - периметр четвёртой клумбы.
И теперь длину изгороди на все четыре клумбы - сумма отдельных.
5) Р = 16+20+18+16 = 70 м на все четыре клумбы - ОТВЕТ
a + b не равно 0, значит, a^2 - ab + b^2 = 1 или a^2 - ab + b^2 - 1 = 0
Теперь вспоминаем, что a^2 + b^2 = a + b:
a + b - ab - 1 = 0
(a - ab) + (b - 1) = 0
(a - 1)(b - 1) = 0
Для того, чтобы произведение было равно нулю, хотя бы один из сомножителей должен быть равен нулю, т.е. хотя бы одно из чисел a, b, равно 1.
Без умаления общности можно считать, что a = 1 (система симметрична относительно замены a на b и наоборот). Докажем, что b = 1.
Подставляем a = 1 в равенство a^2 + b^2 = a + b:
b^2 + 1 = b + 1
b^2 - b = 0
b(b - 1) = 0
b > 0, значит, b = 1, как и требовалось.