1) Пусть равенство 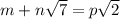 выполнено. Тогда выполнено и равенство
выполнено. Тогда выполнено и равенство 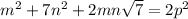 , но слева иррациональное число, а справа целое, противоречие.
, но слева иррациональное число, а справа целое, противоречие.
2) Пусть сразу 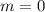 ,
, 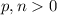 . Тогда нам нужно найти как можно меньшее значение
. Тогда нам нужно найти как можно меньшее значение 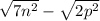 . Мы сможем этого достичь, если числа
. Мы сможем этого достичь, если числа 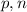 будут достаточно большими, а величина
будут достаточно большими, а величина  достаточно маленькой.
достаточно маленькой.
Найдем такие числа. Пусть 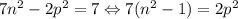 , возьмем
, возьмем 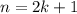 . Получим
. Получим 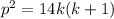 , пусть
, пусть 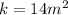 , тогда требуется найти такое
, тогда требуется найти такое 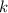 , чтобы
, чтобы 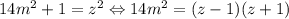 , сделаем последнюю замену:
, сделаем последнюю замену: 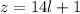 , имеем:
, имеем: 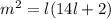 , откуда сразу угадывается решение
, откуда сразу угадывается решение 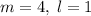 . Возвращаясь к заменам, получим
. Возвращаясь к заменам, получим 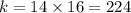 , Значит,
, Значит, 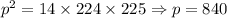 ,
, 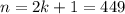 .
.
Теперь осталось проверить: 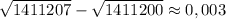 . Итак, решением будет тройка
. Итак, решением будет тройка 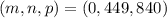
_______________________________________
Рассмотрим сначала числитель неравенства и определим, какой он принимает знак (это можно сделать по причине того, что в числителе отсутствуют неизвестные).Вспомним, что множество значений функции арккосинуса - это ![[ \; 0; \; \pi \; ]](/tpl/images/1358/6614/e7584.png) (а область определения
(а область определения ![[ \; -1; \; 1 \; ]](/tpl/images/1358/6614/9cc29.png) ). Так как
). Так как 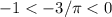 , то такой арккосинус имеет место быть. И его значение положительно.
, то такой арккосинус имеет место быть. И его значение положительно.
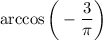 без смены знака и проблемы "деление на ноль".
без смены знака и проблемы "деление на ноль".Теперь посмотрим на логарифм. Его основание и подлогарифмическое выражение (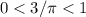 и
и 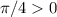 ) соответствуют всем требованиям по ОДЗ. Также, из-за того, что и основание, и подлогарифмическое выражение находятся на промежутке
) соответствуют всем требованиям по ОДЗ. Также, из-за того, что и основание, и подлогарифмическое выражение находятся на промежутке 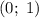 , само значение логарифма больше ноля.
, само значение логарифма больше ноля.
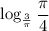 , с равносильным переходом.
, с равносильным переходом._______________________________________
Уравнение принимает вид (после сокращения на логарифм и арккосинус):
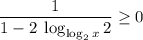
И тут можно вспомнить про ограничения (вообще, можно было их прямо сейчас не писать, и, тем более, не решать, но за пределам скобок было написано "можно"):
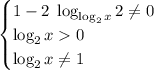
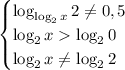
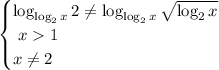
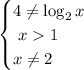
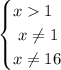
_______________________________________
Теперь заметим, чтобы неравенство выполнялось, необходимо, чтобы:
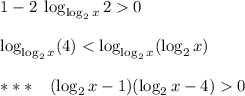
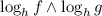 , то
, то 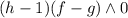 ).
).Дальше - метод интервалов. Первая скобка обноляется при 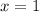 , а вторая - при
, а вторая - при 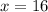 . Знаки на числовой оси тоже можно расставить (отмеченные точки - выколотые):
. Знаки на числовой оси тоже можно расставить (отмеченные точки - выколотые):
+ + + + + - - - - - + + + + +
___________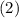 ___________
___________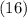 ___________
___________
В пересечении с ОДЗ (актуально 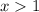 ) имеем вот такое решение:
) имеем вот такое решение:
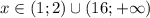
Номер ответа - C)!
_______________________________________
ответ: С)
4 часа
Пошаговое объяснение:
1) Узнаем время затраченное на путь туда
Туда он ехал 8 часов.
2) Нам известно, что скорость поезда на обратном пути была в 2 раза больше, что означает, что время пути сократилось вдвое. Следовательно обратно поезд проехал 400 км за 4 часа.