Т.к. биссектриса делит угл пополам, а мы знаем, что развернутый угл равен 180 градусам; 180:2=90 градусов один угл. 90 градусов это прямой угл.
3)прямые
решение
1) проведём мр║вн.
для δ авн - это средняя линия, т.к. проходит через середины сторон ав и ан.
значит, мр = вн/2 =10/2=5см.
2) проведём ме║ас.
для δ авн отрезок мк - это средняя линия, т.к. проходит через середины сторон ав и вс.
значит, мк = ан/2 =4/2=2см.
в прямоугольнике мрнк противоположные стороны равны, т.е.
мк = рн = 2 см.
отрезок рс = рн + нс = 2см + 10 см = 12 см
3) из прямоугольного δ мрс по теореме пифагора найдём гипотенузу мс.
мс² = мр² +рс²
мс² = 5² + 12²2 = 25 + 144 = 169
мc= √169 =13 см
ответ: б)
Выделяем полные квадраты:
для x:
9(x²-2·3x + 3²) -9·3² = 9(x1-3)²-81
для y:
-16(y²+2·21 + 2²) +16·2² = -16(y1+2)²+64
В итоге получаем:
9(x-3)²-16(y+2)² = 144
Разделим все выражение на 144
(9(x-3)²/144) - (16(y+2)²/144) = 144/144,
((x-3)²/16) - ((y+2)²/9) = 1,
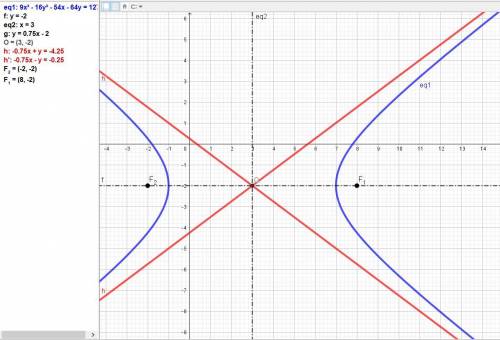
Данное уравнение определяет гиперболу ((x-3)²/4²) - ((y+2)²/3²) = 1
с центром в точке C(3; -2) и полуосями: a = 4 (действительная полуось); b = 3 (мнимая полуось).
Найдем координаты ее фокусов: F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами с учётом центра (3; -2).
Определим параметр c: c² = a² + b² = 16 + 9 = 25.
c = 5.
Координаты фокусов (3 +-5; -2) = (-2; -2) и (8; -2).
Тогда эксцентриситет будет равен: е = с/а = 5/4.
Асимптотами гиперболы будут прямые: у + уо = ±(b/a)(x - xo).
y = ±(3/4)(x - 3) + 2.
биссектриса делит угол пополам , в данном случае 180:2=90 градусов, значит на пряммые углы
ответ: 3) пряммые