В субботу продали 80 кг свеклы, капусты на 20 кг больше, а картофеля в 6 раз больше чем свеклы.
В воскресенье продали 30 кг капусты, свеклы в 5 раз меньше, а картофеля в 9 раз больше чем капусты.
Сколько каждого вида продали за выходные? Сколько всего овощей продали в каждый из дней?
В субботу:
Свекла - 80 кг
Капуста - ? кг, на 20 кг >, чем свеклы (стрелка от Капусты до Свеклы)
Картофель - ? кг, в 6 раз >, чем свеклы (стрелка от Картофеля до Свеклы)
В воскресенье:
Капуста - 30 кг
Свекла - ? кг, в 5 раз <, чем капусты (стрелка от Свеклы до Капусты)
Картофель - ? кг, в 9 раз >, чем капусты (стрелка от Картофеля до Капусты)
Сколько каждого вида продали за выходные? Сколько всего овощей продали в каждый из дней?
В субботу:
1) 80+20=100 (кг) - капусты продали в субботу.
2) 80·6=480 (кг) - картофеля продали в субботу.
В воскресенье:
3) 30:5=6 (кг) - свеклы продали в воскресенье.
4) 30·9=270 (кг) - картофеля продали в воскресенье.
Выходные (Суббота + Воскресенье)
5) 80+6=86 (кг) - свеклы продали за выходные всего.
6) 100+30=130 (кг) - капусты продали за выходные всего.
7) 480+270=750 (кг) картофеля продали за выходные всего.
Допустим, что по двору ходило неизвестное число П поросят и Г гусей
тогда нам ещё известно, что у поросят 4 копыт, а у гусей 2 лапки
⇒ соответственно у нас получается 4П и 2Г
П + Г = 25
4П + 2Г = 70
П + Г = 25 /·2
умножаем на 2 для того чтобы потом вычесть столбиком и найти одно из неизвестных
4П + 2Г = 70
_
2П + 2Г = 50
2П + 0Г = 20
2П = 20 ⇒ П = 20:2=10 - это количество поросят.
2П + 2Г = 50 ⇒ 2 Г=50 - 2П ⇒ Г = (50 - 2П)/2
Г =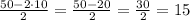 
- это количество гусей.
ответ: на скотном дворе гуляли 15 гусей и 10 поросят.
Если 14616 разделить на 29, то получается целое число (без остатка) 504. Следовательно 14616 кратно 29. (Если одно число делится на другое число без остатка - это и есть кратность)
И второе:
2. Число "y" называется делителем числа "x", когда выполняется условие х/у=R, т. е. нужно доказать, что число 44968 нацело делится на число 56.
Признак делимости на 56: число делится на 56 тогда, когда оно делится на 7 и на 8 одновременно.
Признаков делимости на 7 несколько. воспользуемя одним из них: число делится на 7 тогда и только тогда, когда разность числа десятков и удвоенного числа единиц, взятая по модулю, делится на 7 т.е. 4496 - 16 = 4480 делится на 7 ( 448 - 0 = 448 - делится на 7 ( 44-16=28; 28/7=4) значит 44968 делится на 7
Признак делимости на 8: Число делится на 8 тогда и только тогда, когда число, образованное тремя его последними цифрами, делится на 8 (если число трёхзначное, то оно делится на 8 тогда, когда число единиц, сложенное с удвоенным числом десятков и учетверённым числом сотен, делится на 8) т.е 968 делится на 8 (8+12+36 = 56; 56/8=7) следовательно число 44968 делится и на 8.
Значит оно делится и на 56, то есть 56 - делитель числа 44968
44968/56=803 (всё делится)