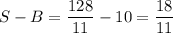Пошаговое объяснение:
Предположим, что в этой пятерке есть нечетные числа.
Сумма трех чисел будет четной в двух случаях:
- если все три числа четные;
- если два числа нечетные, а третье четное.
Подумаем, сколько нечетных чисел может находиться в нашей пятерке чисел. Явно меньше 3-х (если их 3 или более, то сразу выбираем "плохую" тройку чисел - все нечетные, и результат нас не устраивает).
Меньше 3-х - это два нечетных числа. Рассмотрим самый перспективный вариант:
пусть числа aₓ - нечетные числа, bₓ - четные числа.
a₁ a₂ b₁ b₂ b₃
Перебираем варианты:
a₁ + a₂ + b₁ - четная сумма, нас устраивает,
но уже
a₁ + b₁ + b₂ - нечетная сумма
Одно нечетное число - не вариант - сумма двух четных и нашего одного нечетного нечетна.
Т.о. нечетных чисел в пятерке не может быть нисколько.
а) нет
б) нет
в) 18 / 11
Пошаговое объяснение:
Упорядочим числа по возрастанию (a₁ < a₂ < ... < a₁₁). Тогда по условию:
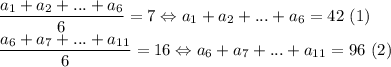
а) Если a₁ = 5, то a₂ ≥ 6, a₃ ≥ 7, ... a₆ ≥ 10. Тогда a₁ + a₂ + ... + a₆ ≥ 5 + 6 + ... + 10 = 45, но сумма шести наименьших чисел равна 42, она не может быть больше или равна 45. Значит, такое невозможно.
б) Если такое возможно, то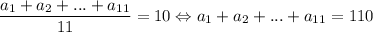 
Сложим уравнения (1) и (2): a₁ + a₂ + ... + a₅ + 2a₆ + a₇ + ... + a₁₁ = 138. Но мы знаем, что a₁ + a₂ + ... + a₅ + a₆ + a₇ + ... + a₁₁ = 110. Тогда 110 + a₆ = 138 ⇔ a₆ = 28 ⇒ a₇ ≥ 29, a₈ ≥ 30, ... , a₁₁ ≥ 33 ⇒ a₆ + a₇ + ... + a₁₁ ≥ 28 + 29 + ... + 33 = 183. Минимально возможная сумма шести наибольших чисел в таком случае равна 183, что больше 96. Значит, такое невозможно.
в) Проведём действия, аналогичные пункту б): 
a₁ + a₂ + ... + a₅ + 2B + a₇ + ... + a₁₁ = 138 ⇒ 11S + B = 138 ⇔ 
⇒ 
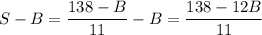. Данное выражение максимально при минимальном значении B.
Если a₆ = B, то в силу различности написанных чисел a₅ ≤ B - 1, a₄ ≤ B - 2, ... , a₁ ≤ B - 5. Тогда 42 = a₁ + a₂ + ... a₆ ≤ 6B - 15 ⇒ 6B ≥ 57 ⇔ B ≥ 9,5 ⇒ B ≥ 10. Тогда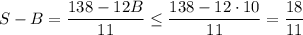 
Действительно, такое значение достигается, например, если были выписаны числа 2, 6, 7, 8, 9, 10, 11, 12, 13, 14, 36. Среднее арифметическое шести наименьших равно 
, среднее арифметическое шести наибольших равно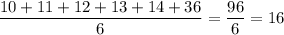 
, среднее арифметическое всех чисел 
, 
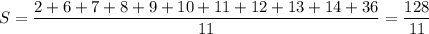