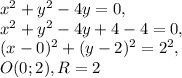
ОБЩЕЕ у всех трех функций.
1. Функция второго порядка - парабола.
2. Область определения - все действительные числа.
D(x)∈(-∞;+∞). Непрерывная, разрывов нет,
ДАНО: -2*х² - х +3.
1. Точки пересечения с осью Х - корни функции - решаем квадратное уравнение. D=25,
x1 = - 1.5, [2 = 1.
2. Промежутки знакопостоянства. Коэффициент при х² < 0 - ветви параболы ВНИЗ.
Положительна - между корней.
3. Первая производная - y'(x) = -4*x - 1. Корень производной: х = - 0,25.
4. Экстремум: максимум - Y(-0.25) = 3.125
5. Возрастает: Х∈(-∞;-0,25], убывает: Х∈[-0.25;+∞)
5. Рисунок к задаче в приложении.
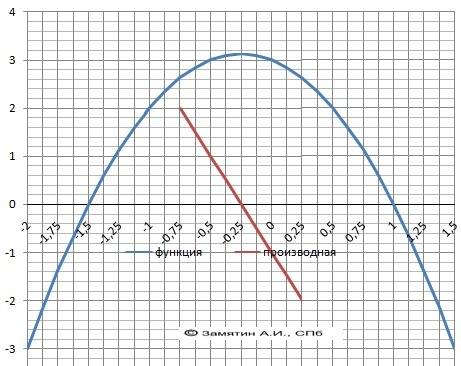
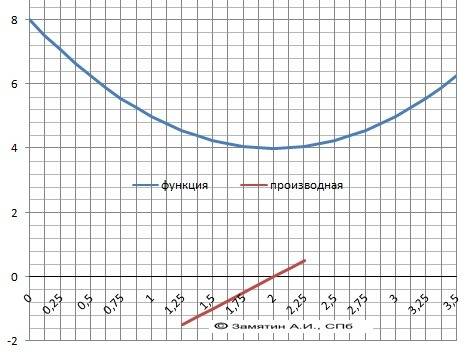
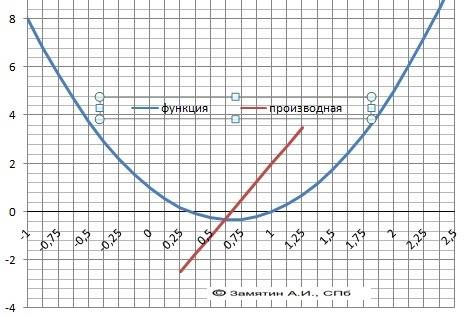
Функция 2.
y =(x-2)² + 4 = x² - 4*x + 8
Корней - нет.
Обозначим четыре части: a; b; c; d.
По условию:
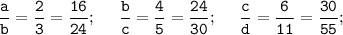
Очевидно, что а = 16; b = 24; c = 30; d = 55
a + b + c + d = 16 + 24 + 30 + 55 = 125
Первая дробь: числитель и знаменатель умножаем на 8, вторая - на 6, третья - на 5. Такой выбор множителей нужен для того, чтобы уравнять значение b, в первом и втором соотношении, и значение с - во втором и третьем соотношении.
Сумма частей, полученная при этом, не обязательно будет равняться исходному числу, но, в любом случае, она будет ему кратной.
Например, исходное число при тех же соотношениях между частями, равно 375. Так как мы в сумме получили 125 "микрочастей", то каждая такая часть, в этом случае, равняется 3, и число 375 разбивается на:
16*3 + 24*3 + 30*3 + 55*3 = 48 + 72 + 90 + 165 = 375.
=========================
Для тех, кто, все-таки, решает эту задачу уравнением..))
Воспользуемся основным свойством пропорции:
3a = 2b; 5b = 4c; 11c = 6d
Сложим левые и правые части:
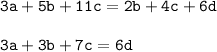
Постараемся в левой части оставить выражение, кратное a+b+c+d, которое, по условию, равно 125:

ответ: 16; 24: 30; 55.