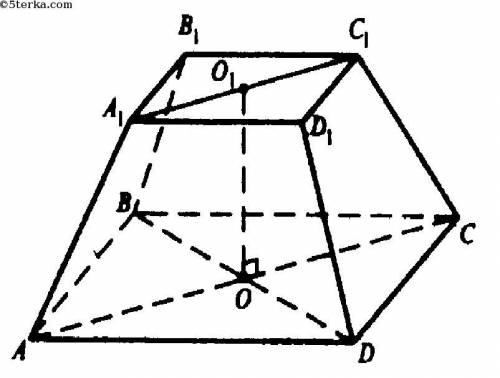
Пусть дана правильная четырехугольная усеченная пирамида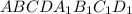 
, где 
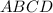и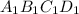 
— квадраты со сторонами соответственно 22 см и 6 см. Боковое ребро пирамиды 
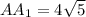см.
Найдем площадь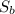 
боковой поверхности заданной пирамиды.
Для того чтобы ее найти, следует найти площадь одной боковой грани (равнобедренной трапеции) и ее умножить на 4.
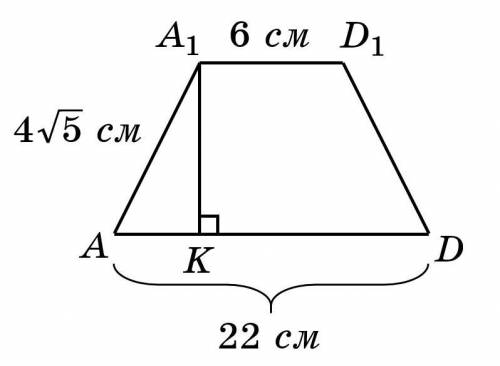
Рассмотрим равнобедренную трапецию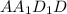 
Проведем в трапеции высоту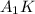 
Найде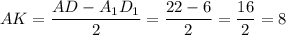м 
см
Рассмотрим прямоугольный треугольник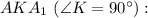 
По теореме Пифагора: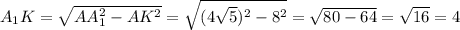 
см.
Следовательно, площадь трапеции равна
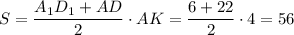см².
Таким образом,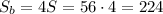 
см².
ответ: 224 см².
а*60=780-420=360
а=360:60=6
2) 450:у+50=70*2=140
450:у=140-50=90
у= 450:90=5
3) 200+20*х=160+200=360
20*х=360-200=160
х=160:20=8
4) х*8-20=1000-300=700
х*8=700+20=720
х=720:8=90
5) b*8-40=410-378=42
b*8=42+40=82
b=82:8=10.25