Пошаговое объяснение:
Раскроем модуль в первом уравнении
-11 ≤ x+2y+1 ≤ 11, (x-a)^2 +(y-2a)^2 = 2+a
-12-x≤2y≤10-x, (x-a)^2 +(y-2a)^2 = 2+a
Получаем систему;:
y ≥ -x/2 - 6
y≤ -x/2 +5
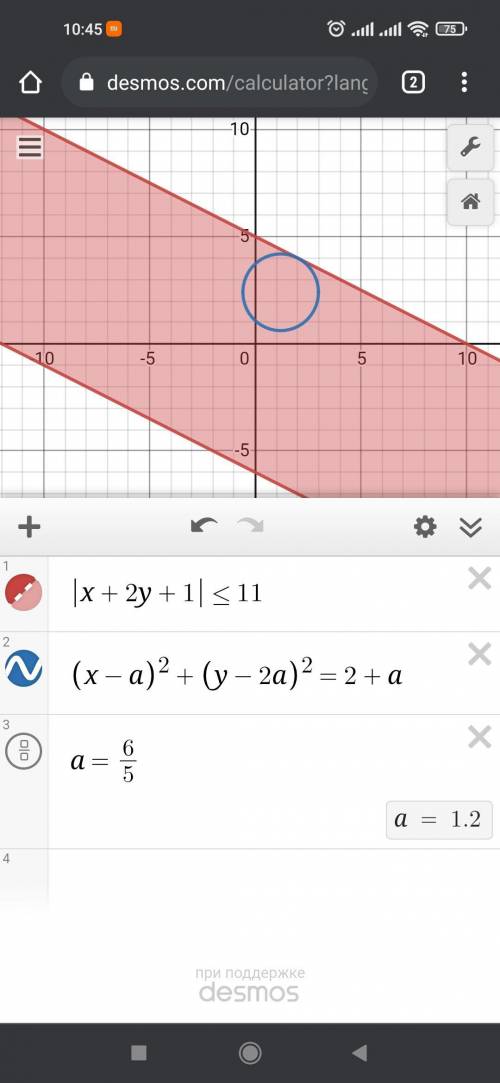
(x-a)^2 +(y-2a)^2 = 2+a → уравнение окружности с радиусом √(2+а) и центром в координатах (а;2а). Радиус ≥0, подставим а=-2 и найдем координаты
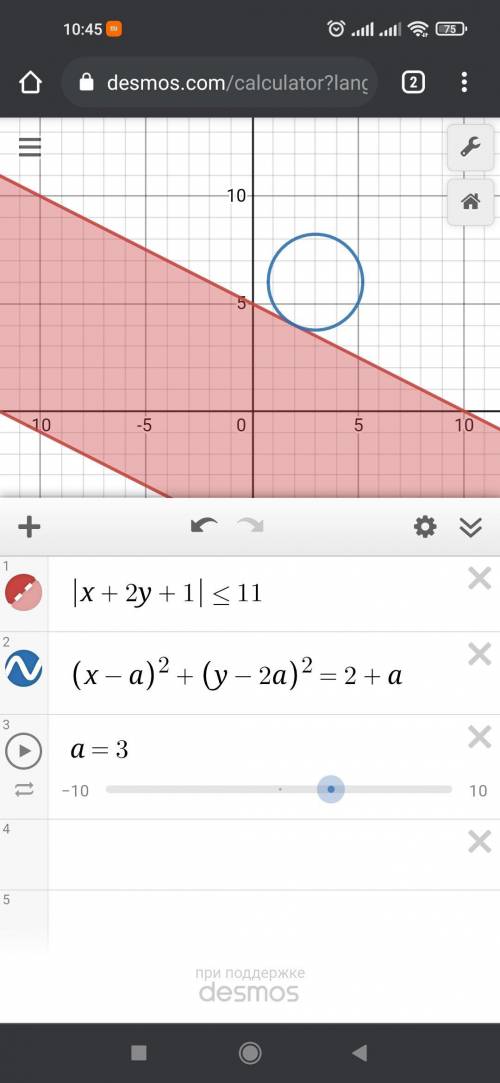
(х+2)^2+(у+4)^2=0. Радиус ноль, координаты точки (-2;-4), что находятся в пределах системы неравенств с прямыми. При увеличении параметра окружность будет двигаться вверх, центр будет лежать на прямой у=2х. Единственное решение будет тогда, когда окружность касается верхней прямой, тоесть 2x=-x/2 +5
5x/2 = 5, x = 2 => y =4. Подставляем в уравнение окружности. (2-а)^2+(4-2а)^2 = 2+а
Раскрываем скобки, решаем и получаем а = 3, а = 6/5. Так как для единственности решения окружность должна касаться прямой у=-х/2+5 сверху, то нам подходит большее значение параметра а=3, ответ а=3
снизу
Пошаговое объяснение:
пусть первый оператор, работая один, может набрать рукопись за Х часов
второй оператор, работая один, может набрать рукопись за 4 часа (он ушел раньше)
тогда за один час первый наберет 1/Х часть рукописи, второй 1/4 часть рукописи
работая вдвоем за один час они наберут 1/Х + 1/4 часть рукописи
работая вдвоем за 2.4 часа они выполнят весь заказ,
т.е. 2.4*(1/Х + 1/4) = 2.4/Х + 0.6 это вся рукопись
2.4/Х + 0.6 = 1 => 2.4/Х = 0.4 => Х = 2.4/0.4 = 6 часов (нужно первому оператору для выполнения задания одному), а за 1 час он набирает 1/6 часть рукописи
вместе они проработали 2 часа, т.е. набрали 2*(1/6 + 1/4) = 2/6 + 1/2 = 2/6 + 3/6 = 5/6 часть рукописи, осталось набрать 1/6 часть рукописи => оставшийся оператор работал еще один час в одиночестве, т.е. задание было выполнено за 3 часа.
ПРОВЕРКА: 1/4 + 1/6 = 3/12 + 2/12 = 5/12 часть рукописи набирают вдвоем за один час
за 2.4 часа наберут вдвоем 2.4*5/12 = 12/12 = 1 целую рукопись
2*1/4 + 2*1/6 + 1/6 = 2/4 + 3/6 = 1/2 + 1/2 = 1 набрали целую рукопись за 2 часа совместной работы и 1 час работы первого оператора...
33*5=165
165=335=500