Пошаговое объяснение:
Проведём наклонную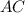 
к плоскости 
.
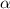Проведём из точки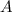 
перпендикуляр 
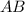к плоскости .
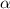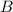- основание перпендикуляра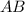
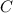- основание наклонной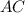
Соединим точк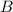и и 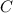и получим проекцию 
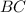наклонной .
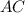Так как 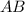- перпендикуляр к плоскости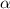 
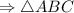- прямоугольный (где 
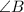- прямой)
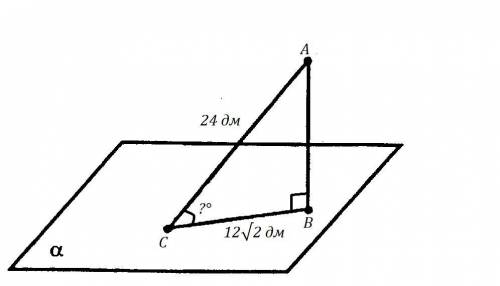
Нам надо найти угол между наклонной 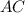и плоскостью - 
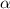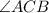
По определению косинуса острого угла в прямоугольном треугольнике,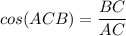 
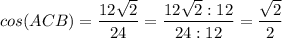
По таблице значений синуса, косинуса, тангенса острых углов получаем:
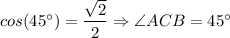
9
Пошаговое объяснение:
( a+b ) × ( a + b + c ) = 5
( b +c ) × ( a + b + c ) = 6
(c + a) × ( a + b + c ) = 7
для удобства заменим ( a + b + c ) = t и в скобочки с думая слогаемыми прибавим и вычтем недостающее
( a + b + c - c ) × t = 5 => ( t - c ) × t = 5 => t^2 - c×t = 5
( b + c + a - a ) × t = 6 => ( t - a ) × t = 6 => t^2 - a×t = 6
( c + a + b - b ) × t = 7 => ( t - b ) × t = 7 => t^2 - b×t = 7
сложим их все: 3×t^2 - c×t - a×t - b×t = 5 + 6 + 7
3×t^2 - t (c + a + b) = 18
3×t^2 - t×t = 18
2×t^2 = 18
t^2 = 9
(ну t^2 = ( a + b + c )^2 что и надо найти)
У нас известна гепотенуза = 5см.
и катет = 3 см.
Соответственно второй катет = 5-3=2 см.
Площадь прямоугольного треугольника равна половине произведения катетов треугольника: S=1/2 ab
1/2*3*2=3см^2 площадь одного треугольника
3см^2 * 2 =6 cм^2 площадь двух треугольников
5*5=25см^2 площадь квадрата
25+6=31см^2 площадь трапеции