Пошаговое объяснение:
если на отрезке
y''(x) > 0, то функция вогнута на этом отрезке
y''(x) < 0, то функция выпукла на этом отрезке
найдем вторую производную от у(х)
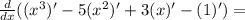
= 3(x²)' -10(x)' = 6x -10
теперь посмотрим, есть ли на отрезке [1;2] точки, где вторая производная меняет знак
6х-10 = 0 ⇒ х = 10/6
в этой точке вторая производная меняет знак, значит и функция меняет выпуклость
посмотрим знак возле этой точки х = 10/6; слева от нее y''(1) <0; справа от нее y'' (2) >0
таким образом
на [1; 10/6) функция выпукла
на (10/6; 2] функция вогнута
точка х = 10/6 - точка перегиба графика функции
-0.5
Пошаговое объяснение:
Геометрический смысл производной: производная функции в точке x0 есть тангенс угла наклона касательной к этой функции, проведенной в точке x0. Угол наклона считают против часовой стрелки от положительного направления оси абсцисс, который мы обозначим за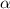 
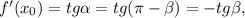где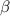 
- угол смежный с .
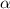Жирные точки на прямой поставлены для удобного вычисления тангенса угла бета. Его легко можно посчитать, если опустить вертикальную линию вниз из левой жирной точки, а из правой жирной точки горизонтальную линию. Тогда эти две точки и точка пересечения проведенных линий образуют прямоугольный треугольник с катетами 3 и 6. Тангенс угла определяется как отношение катета, противолежащего углу, к прилежащему катету: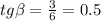 
. Таким образом,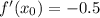
б) 5*5=25
в) 2+2+6+6=16
г) 5+5+5+5=20
дальше не изучал...