ответ: 32
Пошаговое объяснение:
Т.к. турнир закончился когда еще не все партии, то точно есть хотя бы одна неоконченная партия. Рассмотрим игроков, которые должны были играть эту партию. Обозначим их А и Б.
Составляя все четверки, в которые входят игроки А и Б, мы получим, что в этих четверках всегда проведена игра между парой, которая подставлена в четверку к паре А и Б.
Т.е. остальные 33 игрока полностью отыграли между собой все матчи.
Из этих 33 игроков выберем игрока В, который не играл с А или Б. Тогда подставляя остальных 32 игроков в четверку с тройкой А, Б и В мы получим, что эти 32 игрока отыграли и с А и с Б, т.е. полностью отыграли все матчи.
Таким образом минимальное количество игроков каждый из которых сыграл со всеми участниками турнира равно 32.
Покажем, что 32 участника это возможный результат.
Простой пример - сыграны все матчи, кроме А - Б и Б - В.
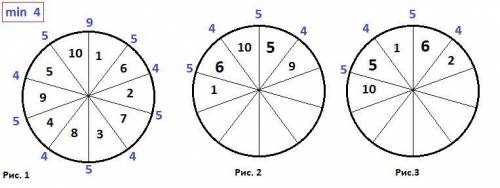
4 - наибольшее возможное значение величины, равной наименьшей из разностей между номерами соседних (по кругу) секторов. Один из вариантов расположения номеров секторов на рис.1.
5 и более получить невозможно, так как для числа 5 с одной стороны можно расположить сектор с номером 10 (10-5=5), а с другой стороны получить разность, более 4, нельзя, так как 5-1=4 и 9-5=4.
Аналогично для числа 6. Если с одной стороны можно получить разность 6-1=5, то с другой стороны более 4 не получится, так как 10-6=4 и 6-2=4. Рис.2 и рис.3
100-50=50 количество апельсинов вообще
так как 2 ящика, то 50:2=25 кг апельсинов в каждом ящике