Пошаговое объяснение:
Алгоритм решения задач на составление уравнений в 5 классе.
Многие задачи в 5 классе решаются с уравнений. От учеников при этом требуется выяснить все величины, участвующие в задаче, отделить известные от неизвестных, установить зависимость между ними, выбрать одну из них для составления уравнения.
При решении задач на составление уравнений можно выделить три этапа:
распознавание величин, участвующих в задаче;
установление зависимостей между величинами;
запись одной величины через другую.
На первом этапе происходит знакомство с всевозможными величинами (стоимость, масса, путь, скорость, время и т.д.). Я читаю несколько предложений и учеников установить, о каких величинах идёт речь в каждом предложении. На втором этапе ученики устанавливают, в каком случае величины суммируются, а в каком случае они вычитаются. Я говорю: в задачах, где требуется сравнить величины, встречаются такие слова: «больше», «меньше», «дешевле», «дороже», «выше», «ниже», «быстрее», «медленнее» и т.д. Узнать же, насколько одна величина больше или меньше другой можно действием вычитания. А на суммирование величин указывают следующие слова: «всего собрали», «всего сделали», «общая масса» и т.д.
Итак, ученик и выслушивают предложения, определяют о каких величинах идёт речь, устанавливают: сравниваются ли они или суммируются и схематически записывают зависимость между ними. Например:
Путь, пройденный путешественниками навстречу друг другу за одно и тоже время равен 18км.
Величины: S1 – путь первого путешественника,
S2 – путь второго путешественника.
S1 + S2 = 18
2) Слонёнок и слониха вместе весят 7200 кг.
Величины: m1 – масса слонихи,
m2 – масса слонёнка.
m1 + m2 = 7200
Бутылка с виноградным соком стоит 60 коп.
Величины: р1 - стоимость бутылки,
р2 - стоимость сока.
р1 + р2 = 60
За одно и тоже время первый турист на 5 км больше, чем второй.
Величины: s1 – путь первого туриста,
s2 – путь второго туриста.
s1 – s2 = 5
Затем ученикам даётся схема решения задач на составление уравнений:
перечислить величины, данные в условии задачи.
выбрать меньшую величину из неизвестных величин и обозначить через х.
остальные неизвестные выразить через меньшую величину, т.е. через х.
выяснить сравниваются или суммируются величины.
составить схему уравнения.
Эта схема позволяет ученикам увидеть закономерности между величинами.
Задача: школьники собрали всего 1650 кг картофеля, причём до обеда было собрано в 2 раза больше, чем после обеда. Сколько картофеля собрали школьники после обеда?
Ученики читают условие задачи и устанавливают, что
в условие задачи входят величины масса картофеля, собранного до обеда и масса картофеля, собранного после обеда, общая масса собранного картофеля.
Масса картофеля, собранного после обеда меньше. Её принимаем за х.
Тогда масса картофеля, собранного до обеда, равна 2х кг.
1650 – сумма величин, т.к. в задаче говорится, что всего собрали 1650кг.
Составляется уравнение: 2х + х = 1650.
Итак, этот алгоритм решения задач на составление уравнений учит учеников видеть величины, заданные в условии задачи, и вскрывать связи между ними. А это формированию навыка самостоятельно анализировать новые частные случаи без дополнительного объяснения.
Задание № 1:
На сколько нулей оканчивается значение произведения 20^50*50^20?
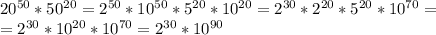
2 в некой степени, очевидно, не заканчивается на 0. Значит, число нулей - 90.
ОТВЕТ: 90
Задание № 2:
Сколько существует двузначных чисел, которые после перестановки цифр увеличиваются на 75%?
РЕШЕНИЕ: Пусть было число АВ=10а+b. После перестановки получили число BA=10b+a. По условию:
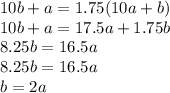
Значит, если в числе цифра десятков в 2 раза больше цифры единиц, то оно попадает под наше условие.
Это числа: 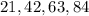
ОТВЕТ: 4 числа
Задание № 3:
Решите уравнение: |||x|−5|−5|=5. Назовите наибольший корень уравнения.

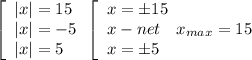
ОТВЕТ: 15
Задание № 4:
В коробке лежат чёрные, белые и красные шарики. Чёрных больше, чем 7, а белых меньше, чем 7. Вместе чёрных и красных в 2 раза больше, чем белых, а белых и красных ровно столько, сколько чёрных. Сколько всего шариков?
РЕШЕНИЕ: Пусть черных с, белых b, красных k.
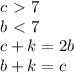
Складываем уравнения:
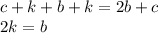
Подставляем во второе:
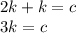

Единственное возможное целое k - число 3.
Тогда k+c+b=k+3k+2k=6k=6*3=18 шариков
ОТВЕТ: 18 шариков
Задание № 5:
Стоя неподвижно на ступени эскалатора в метро Ваня поднимается наверх за одну минуту. Взбегая по ступеням неподвижного эскалатора, он добирается до верха за 40 секунд. За какое время Ваня поднимается наверх, если начинает взбегать по ступеням эскалатора, движущегося вверх? Дайте ответ в секундах.
РЕШЕНИЕ: Пусть длина расстояния L.
Если Ваня стоит неподвижно на ступени эскалатора, то скорость движения равна L/60. (Считаем в секундах, в минуте 60 секунд).
Если Ваня взбегает по ступеням неподвижного эскалатора, то скорость движения равна L/40.
Когда Ваня бежит по ступеням движущегося эскалатора, то скорости Вани и эскалатора суммируются: L/60+L/40. Тогда время определяется отношением длины к скорости:

ОТВЕТ: 24 секунды
Задание № 6:
Встретились три охотника и сварили кашу. Первый дал две кружки крупы, второй — три кружки крупы, а у третьего крупы не было. Но зато он дал охотникам 30 рублей в качестве платы за кашу. Все кашу ели поровну. Сколько рублей достанется второму охотнику, если их разделить по справедливости?
РЕШЕНИЕ: Так как 3 порции каши готовились из 5 кружек крупы, то одна порция составляет (5/3) кружки.
Первый дал две кружки крупы, значит, он имел право получить две кружки каши. Однако он взял только (5/3) кружки. 2-5/3=1/3 кружки – первый передал третьему
Второй дал три кружки крупы, значит, он имел право получить три кружки каши. Однако он взял только (5/3) кружки. 3-5/3=4/3 кружки – второй передал третьему
Видно, что второй передал третьему в 4 раза больше каши, чем первый. Значит и денег он получит в 4 раза больше. Деньги делим в отношении 1:4, то есть всего 5 частей. 30/5*4=24 рубля
ОТВЕТ: 24 рубля
Задание № 7:
Отрезок 50 см разделён на четыре неравных отрезка. Расстояние между серединами средних отрезков равно 10 см. Найдите расстояние между серединами крайних отрезков. Дайте ответ в сантиметрах.
РЕШЕНИЕ: Расстояние между серединами крайних отрезков представляет собой полусумму длин крайних отрезков и сумму длин средних отрезков.
Так как расстояние между серединами средних отрезков равно 10 см, то сумма их длин равна 2*10=20 см.
Оставшаяся длина – это сумма длин крайних отрезков: 50-20=30 см. Их полусумма тогда равна 30/2=15 см
20+15=35 см
ОТВЕТ: 35 см
2)9-6=3(см)-ширина прямоугольника
3)6*3=18(см)-площадь прямоугольника
ответ:18см