Математика: Быстро чему равна площадь треугольника

Быстро чему равна площадь треугольника

👇

Увидеть ответ

Ответ:

Kiska41384

22.06.2022

S=1/2*a*h
S=1/2*a*b (в прямоугольном треугольнике)
S=(a^2*√3)/2 (в равностороннем)

4,7(33 оценок)

Открыть все ответы

Ответ:

pandamashenka

22.06.2022

ответэлементами множеств а, p, q являются натуральные числа, причём p = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21}, q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}. известно, что выражение

((x ∈ p) → (x ∈ a)) ∨ (¬(x ∈ a) → ¬(x ∈ q))

истинно ( т. е. принимает значение 1) при любом значении переменной х. определите наименьшее возможное значение суммы элементов множества a.

пояснение.

раскроем две импликации. получим:

(¬(x ∈ p) ∨ (x ∈ a)) ∨ ((x ∈ a) ∨ ¬(x ∈ q))

(¬(x ∈ p) ∨ (x ∈ a) ∨ ¬(x ∈ q))

¬(x ∈ p) ∨ ¬(x ∈ q) 0, только когда число лежит в обоих множествах. значит, чтобы все выражение было истинно, нужно все числа, лежащие в p и q, занести в а. такие числа 3, 9, 15 и 21. их сумма 48.

ответ: 48

пошаговое объяснение:

4,7(5 оценок)

Ответ:

морол

22.06.2022

Представим себе двудольный граф: слева вершины, обозначающие студентов, справа — вопросы. Если студент ответил на вопрос, то между этим студентом и этим вопросом проведем ребро.

Рассмотрим первую пару вопросов (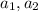 $a_{1},a_{2}$ ). Для них по условию найдется хотя бы 6 студентов, каждый из которых ответил правильно ровно на один из этих двух вопросов. Пусть это множество из хотя бы 6 студентов называется 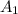$A_{1}$ . Тогда остальных студентов (тех, что не удовлетворяют описанному требованию) не больше 5 — это множество 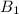$B_{1}$ . Рассмотрим следующую пару вопросов ( 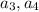$a_{3},a_{4}$ ,попарно отличных от предыдущих). Тогда 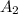$A_{2}$ имеет с 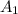$A_{1}$ хотя бы одно пересечение. Поэтому для пары 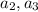$a_{2},a_{3}$ будет хотя бы одно ребро из множества 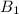$B_{1}$ . Рассматривая далее пары 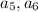$a_{5},a_{6}$ и соответственно пары 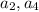$a_{2},a_{4}$ "берем" еще один элемент из 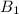$B_{1}$ . Так можно продолжать до тех пор, пока все элементы из 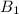$B_{1}$ , коих не больше пяти, не будут взяты. То есть всего можно добавить 2*5=10 вопросов дополнительно к 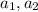$a_{1}, a_{2}$ . То есть всего не более 12.

Примечание: множество 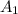$A_{1}$ делится на два множества, из каждого идут ребра к вопросам 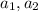$a_{1},a_{2}$ , но из каждого к ровно одному. Для того, чтобы мы могли всегда изымать элементы из 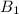$B_{1}$ надо всего лишь без ограничения общности потребовать, чтобы ребро из 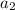$a_{2}$ шло в наибольшее из множеств, на которое делится 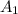$A_{1}$ . Тогда наименьшее из этих множеств деления не превосходит 5.