Пошаговое объяснение:
1
1) 2mn=2m³n⁴ /m²n³ ; 1 /m²n = n² /m²n³ ; 1 / mn³ = m /m²n³
2) 3 /2x² = 18xy⁴/12x³y⁴; 3 /4 x³y = 9y³/12x³y⁴ ; 5 / 6xy⁴= 10x²/12x³y⁴
2
1) 1 / 4b²- 9 u b /2b+3
1 / 4b²- 9 =1 /(2b-3)(2b+3)
b /2b+3 = b(2b-3) / (2b-3)(2b+3) =2b²-3b / (2b-3)(2b+3)
2) 1 / x²-25 u 4 / 5-x
1 / x²-25 = 1 / (x-5)(x+5)
4 / 5-x = - 4(x+5) / (x-5)(x+5) = - 4x+20 /(x-5)(x+5)
3
1) 1 / y²-9 = y+3 / (y-3)(y+3)²
1/(y+3)² = y-3 / (y-3)(y+3)²
2) 1 /25x²-10x+1 = 1 /(5x-1)² (5x+1)² / (5x-1)²(5x+1)²
1 / 1+10x+25x²= 1/ (5x+1)² (5x-1)² /(5x-1)²(5x+1)²
1 /1-25x² = - 1 / (5x-1)(5x+1) -(5x-1)(5x+1) /(5x-1)²(5x+1)²=
= - 25x-1 /(5x-1)(5x+1)
-5 < a < -1/2 или 3 < a < 7/2
Пошаговое объяснение:
Сделаем замену x + 4/x = y. Получается квадратное уравнение:
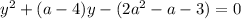
Домножим на 4 и выделим полный квадрат. Получится разность квадратов, которую преобразуем в произведение:
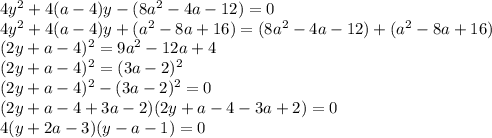
Если вам не нравится такой можете использовать дискриминант или угадать корни, пользуясь теоремой Виета. Так или иначе, корни этого уравнения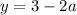 
и 
.
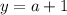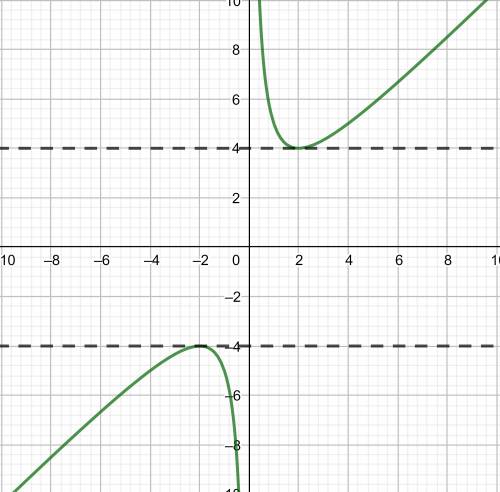
Когда мы вернемся обратно к иксам, нужно будет определять количество корней уравнения вида x + 4/x = t. Нарисуем график функции f(x) = x + 4/x. Это нечетная функция, сфокусируемся на x > 0.
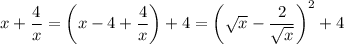
Минимальное значение f(x) равно 4, достигается при x = 2. При x > 2 функция неограниченно возрастает (поскольку выражение в скобках положительно и оба слагаемых возрастают), а так как уравнение переходит само в себя при замене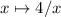 
, то при 0 < x < 2 функция убывает от бесконечности.
При x < 0 всё получается симметрично относительно начала координат. График показан на картинке.
Итак, x + 4/x = t не имеет решений, если -4 < t < 4, одно решение, если t = -4 или t = 4, и два решения во всех остальных случаях.
Осталось понять, когда у исходного уравнения будет два решения.
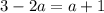и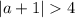 
Первое равенство выполнено при a = 2/3, тогда у уравнения нет решений. Не подходит
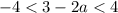и 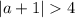Первое неравенство дает -1/2 < a < 7/2, второе a > 3 или a < -5. Пересечение: 3 < a < 7/2.
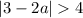и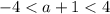 
Первое неравенство: a > 7/2 или a < -1/2, второе: -5 < a < 3. Пересечение: -5 < a < -1/2.
3 - 2a = 4, a + 1 = -4Нет решений
3 - 2a = -4, a + 1 = 4Нет решений
