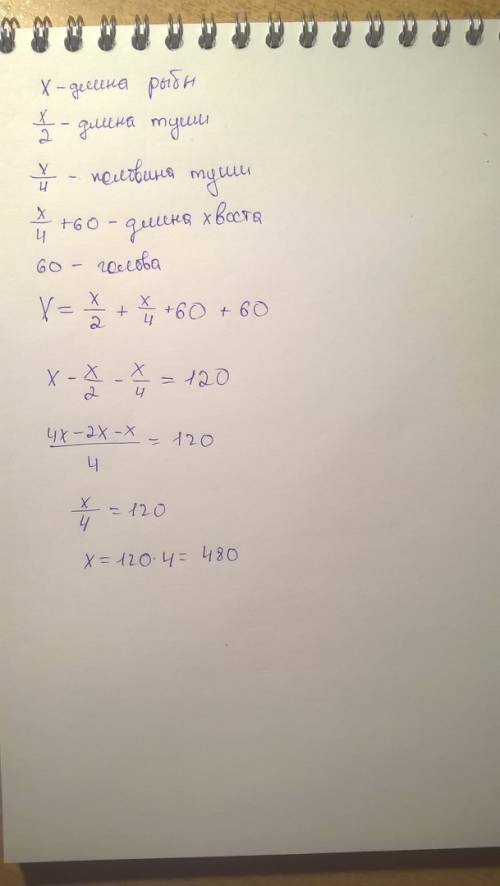
(2; 0,5)
Пошаговое объяснение:
Очевидно, К=2 нам не подходит, т.к. такая прямая (F(x) = kx - линейная функция, график прямая) будет совпадать с 2х.
Рассмотрим график; чтобы было три пересечения, прямая должна пересекать все три "куска" графика.
Первую часть, у=2х, пересекает при К!=2.Вторую часть, у=2, пересекает при всех К принадлежащих интервалу (2;0.5) - 0.5 получаем из уравнения 2=4К (берем "граничное" положение (при котором УЖЕ нельзя найти три пересечения) F(x)=kx и подставляем.Третью часть пересекает при соблюдении первого условия, т.к. если прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую.Имеем К!=2 и 2<K<0,5 => К принадлежит (2; 0,5).
1) найдем внутренний угол Д: 180-125=55°
Найдем угол С: С=180°-(90+55°)=35°
2) в треугольнике КМТ оба катета равны, значит, углы МКТ и КТМ равны 45°. Найдём угол Т в треугольнике KTS: Т=180-45=135°.
Угол S = 180°-(20°+135°)=25°.
3) Катет АС в два раза меньше гипотенузы АД, значит, угол Д=30°. Угол А=180°-(90°+30°)=60°
4) Первый острый угол – х; второй острый угол – 4х.
х+4х+90=180
5х=90
х=18° - первый острый угол
4×18°=72° - второй острый угол
5) Начертим прямоугольный треугольник АСВ, где угол С=90°.
Проведем биссектрисы СМ и ВК, которые пересекаются в точке О.
Рассмотрим треугольник СОВ, где угол С=45°, угол О=132°, угол В = 180°-(45°+132°)=3°.
Значит, в треугольнике АСВ угол В=6°.
Найдем угол А: А=180°-(90°+6°)=84°.
Итог: треугольник АСВ имеет углы: С=90°; В=6°; А=84°