Был произведён один выстрел.
Гипотезы:
A₁ - стрелял первый стрелок,
A₂ - стрелял второй стрелок,
A₃ - стрелял третий стрелок.
Событие А - после выстрела мишень поражена.
P(A₁) = P(A₂) = P(A₃) = 1/3.
P(A|A₁) = 0,3
P(A|A₂) = 0,5
P(A|A₃) = 0,8
По формуле полной вероятности
P(A) = P(A₁)·P(A|A₁) + P(A₂)·P(A|A₂) + P(A₃)·P(A|A₃) =
= (1/3)·0,3 + (1/3)·0,5 + (1/3)·0,8 = 1,6/3.
По формуле Байеса
P(A₂·A) = P(A₂)·P(A|A₂),
P(A₂·A) = P(A)·P(A₂|A),
P(A)·P(A₂|A) = P(A₂)·P(A|A₂)
P(A₂|A) = P(A₂)·P(A|A₂)/P(A)
P(A₂|A) = ( (1/3)·0,5)/(1,6/3) = 0,5/1,6 = 5/16 = 0,3125.
ответ. 0,3125.
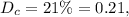 а долю масла в сливках, как
а долю масла в сливках, как 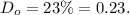
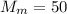 кг молока. Посчитаем, какую массу масла
кг молока. Посчитаем, какую массу масла 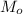 можно из него получить.
можно из него получить.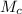 , которую можно собрать с молока, воспользуемся простым правилом: умножаем на число процентов в доле и делим на сто процентов:
, которую можно собрать с молока, воспользуемся простым правилом: умножаем на число процентов в доле и делим на сто процентов: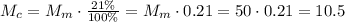 кг.
кг.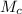 мы просто умножили
мы просто умножили 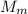 на
на 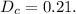
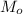 , которую можно выделить из собранных сливок, воспользуемся теми же правилами:
, которую можно выделить из собранных сливок, воспользуемся теми же правилами: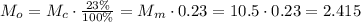 кг масла
кг масла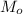 мы просто умножили
мы просто умножили 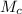 на
на 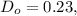 т.е., учитывая расчёт **(A)** мы умножили
т.е., учитывая расчёт **(A)** мы умножили 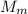 на
на 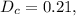 а затем на
а затем на 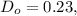 и в самом деле:
и в самом деле: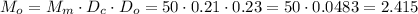 кг масла
кг масла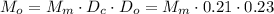 ;
;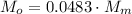 ;
;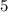 кг
кг 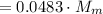 ;
;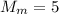 кг
кг 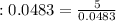 кг
кг 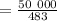 кг ;
кг ;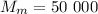 кг
кг 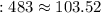 кг ;
кг ;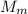 из уравнения **(С)** :
из уравнения **(С)** :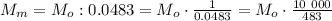 и опять же найдем, что:
и опять же найдем, что: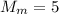 кг
кг 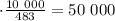 кг
кг 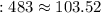 кг ;
кг ;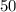 кг молока можно получить
кг молока можно получить 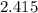 кг масла.
кг масла.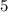 кг масла нужно
кг масла нужно 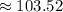 кг молока.
кг молока.
2)44×19=836