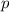и 
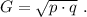
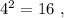а произведение двух самых больших равно 
»
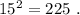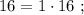
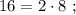
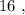т.е.: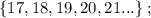 
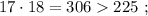
каждое – будет, очевидно, больше чем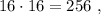 
т.е. больше 
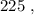а значит, при выборе минимальных чисел в виде 
и – подобрать остальные числа невозможно.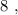
т.е.: 
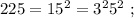
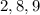и 
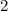и 
и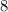 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы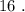 
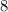и никаких натуральных чисел нет. и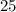 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы 
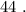
Точки экстремума функции находятся внутри отрезка [-1;4]. Тогда для определения наименьшего и наибольшего значений функции на заданном отрезке надо искать значения функции в точках экстремума и на краях отрезка.
у(-1)=3+2=5-наибольшее значение функции на отрезке [-1;4];
у(0)=0
y(1)=3-2=1
y(4)=48-128=-80-наименьшее значение функции на отрезке [-1;4].