1.Область определения D(x) - непрерывная Х∈(-∞;+∞).
Вертикальных асимптот - нет.
2. Пересечение с осью Х. Y=0 при х = 0.
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = +∞.
Горизонтальных асимптот - нет.
5. Исследование на чётность.Y(-x) = - Y(x).
Функция нечётная.
6. Производная функции.
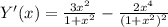
Корень при Х=0. Схема знаков производной.
(-∞)__(>0)__(х=0)_(<0)__(+∞)
7. Локальные экстремумы.
Максимума и минимума – нет.
8. Интервалы монотонности.
Возрастает на всем интервале определения- Х∈(-∞;+∞)
9. Вторая производная - Y"(x).
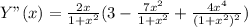
Корни производной - точки перегиба: х1 = 0, х2= -√3, х3= √3.
9. Выпуклая “горка» Х∈(-√3;0)∪√3;+∞), Вогнутая – «ложка» Х∈(-∞;-√3)∪(0;√3).
10. Область значений Е(у) У∈(-∞;+∞)
11. Наклонная асимптота. Уравнение: lim(∞)(k*x+b – f(x).
k=lim(∞)Y(x)/x = x²/(1+x²) = 1. Уравнение: Y =x/
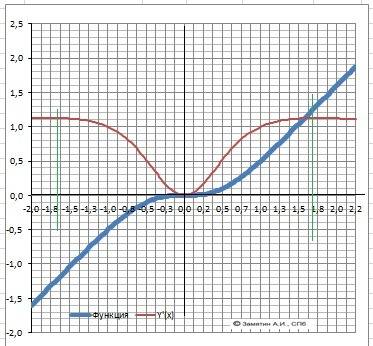
12.График в приложении.
МатБюро Теория вероятностей Учебник по теории вероятностей Сложение и умножение вероятностей
Учебник по теории вероятностей
1.4. Сложение и умножение вероятностей
Полезная страница? Сохрани или расскажи друзьям
Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записывается как A⊂B.
События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается очевидно: А = В.
Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.
Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
P(A+B)=P(A)+P(B).
Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:
P(
n
∑
i=1 Ai)=
n
∑
i=1 P(Ai).
Если случайные события A1,A2,...,An образуют полную группу несовместных событий, то имеет место равенство P(A1)+P(A2)+...+P(An)=1. Такие события (гипотезы) используются при решении задач на полную вероятность.
Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.
Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле
P(A+B)=P(A)+P(B)−P(A⋅B).
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:
P(A⋅B)=P(A)⋅P(B).
Вероятность произведения зависимых событий вычисляется по формуле условной вероятности.
Примеры решений задач с событиями
Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.
Решение. Обозначим события: А – вынули белый шар из первого ящика,
;