У двух мальчиков 15 яблок. Пусть у первого Х яблок, тогда у второго 15 -Х яблок.
Если первый мальчик даст второму 4 яблока, то унего станет Х - 4 яблока,
а увторого тогда станет 15 -Х + 4 = 19 -х яблок , и у первого яблок будет в 2 раза меньше чем у второго =>
2*(Х - 4) = 19 -х
2Х - 8 = 19 -х
2Х + х = 19 + 8
3Х = 27
Х = 27:3
Х = 9 (яблок у первого)
у второго 15 -Х = 15 - 9 = 6 (яблок у второго)
ответ: у первого мальчика 9 яблок, у второго мальчика 6 яблок.
Большая сторона первоначального прямоугольника x.
Есть два возможный варианта: 1) прямоугольник разрезали по меньшей стороне; 2) прямоугольник разрезали по большей стороне. Рассмотрим их оба:
1) пусть одна сторона первого прямоугольника y, тогда вторая 6-y. Вторые стороны у обоих x.
Площади: xy кв.ед. у первого, x·(6-y) кв.ед. у второго. У первого в 3 раза больше:
xy = 3x·(6-y)
Периметры: (x+y)·2 у первого, (x+6-y)·2 у второго. У первого в 2 раза больше:
(x+y)·2 = 2·(x+6-y)·2
Составим и решим систему уравнений:

Большая сторона первоначального прямоугольника 1,5.
2) пусть одна сторона первого прямоугольника y, тогда вторая x-y. Вторые стороны у обоих 6.
Площади: 6y кв.ед. у первого, 6(x-y) кв.ед. у второго. У первого в 3 раза больше:
6y = 3·6(x-y)
Периметры: у первого (y+6)·2, у второго (x-y+6)·2, у первого в 2 раза больше:
(y+6)·2 = 2·(x-y+6)·2.
Составим и решим систему уравнений:
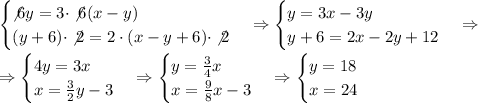
Большая сторона первоначального прямоугольника 24.
ответ: 1,5 или 24.
-x²+4x-1=-x-1
x²-5x=0 => x=0 x=5. то есть точки пересечения (0,-1) и (5,-6). Точки пересечения под осью ОХ. Поэтому надо поднять наши графики на 6 выше. Тогда площадь не изменится и целиком будет выше ОХ.
y=-x-1+6=-x+5
y=-x²+4x-1+6=-x²+4x+5
точки пересечения будут (0,5) и (5,0)
S=∫₀⁵(-x²+4x+5)dx-∫₀⁵(-x+5)dx=(-x³/3+4x²/2+5x)|₀⁵-(-x²/2+5x)|₀⁵
=-125/3+50+25+25/2-25=