нет
Пошаговое объяснение:
Если по условию, a+b делится на с (при условии, что a,b и с - натуральные), то при данном делении получится некоторое натуральное число!
Тогда перепишем условие в таком виде:
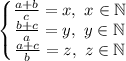
Если a+b+c=2021, то
a+b=2021-c
b+c=2021-a
a+c=2021-b
Подставим в систему и почленно поделим:
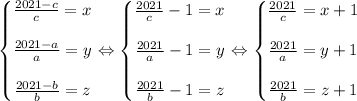
Так как x, y и z натуральные, значит x+1, y+1 и z+1 тоже натуральные числа! То есть, в последней системе во всех трех уравнениях, правые части - это натуральные числа, значит и левые части - тоже натуральные числа!
Таким образом, если (2021/с), (2021/b), (2021/c) ∈ N, то числа а, b и с - это делители числа 2021
2021=1*43*47
Каждое из чисел a, b или с может принимать значения: 1; 43; 47; 2021.
Перебирая эти варианты, мы выясним, что в сумме 2021 никак не получится!
Називний п’ятнадцять
Родовий п’ятнадцяти, п’ятнадцятьох
Давальний п’ятнадцяти, п’ятнадцятьом
Знахідний п’ятнадцять, п’ятнадцятьох
Орудний п’ятнадцятьма, п’ятнадцятьома
Місцевий на/у п’ятнадцяти, п’ятнадцятьох
Чоловічий, середній рід Жіночий рід
Називний сорок два сорок дві
Родовий сорока двох сорока двох
Давальний сорока двом сорока двом
Знахідний сорок два (двох) сорок дві (двох)
Орудний сорока двома сорока двома
Місцевий на/у сорока двох на/у сорока двох
Називний п’ятдесят шість
Родовий п’ятдесяти (п’ятдесятьох) шести (шістьох)
Давальний п’ятдесяти (п’ятдесятьом) шести (шістьом)
Знахідний п’ятдесят (п’ятдесятьох) шість (шістьох)
Орудний п’ятдесятьма (п’ятдесятьома) шістьма (шістьома)
Місцевий на/у п’ятдесяти (п’ятдесятьох) шести (шістьох)
Називний сто дванадцять
Родовий ста дванадцяти (дванадцятьох)
Давальний ста дванадцяти (дванадцятьом)
Знахідний сто дванадцять (дванадцятьох)
Орудний ста дванадцятьма (дванадцятьома)
Місцевий на/у ста дванадцяти (дванадцятьох)
Називний дев’яносто вісім
Родовий дев’яноста восьми (вісьмох)
Давальний дев’яноста восьми (вісьмом)
Знахідний дев’яносто вісім (вісьмох)
Орудний дев’яноста вісьма (вісьмома)
Місцевий на/у дев’яноста восьми (вісьмох)