и 
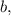то ничего не изменится, всё будет работать как прежде.
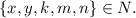
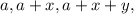чтобы![( [ a + 1 ] + x + y ) | ( 2a+x ) ,](/tpl/images/0497/6250/3dbb9.png)
![( [ a + 1 ] + x ) | ( 2a+x+y )](/tpl/images/0497/6250/bcfc5.png)
и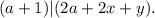
![k ( [ a + 1 ] + x + y ) = 2a + x](/tpl/images/0497/6250/3a31a.png)
;![(k-1) x + ky = 2a - k [ a + 1 ]](/tpl/images/0497/6250/d1c79.png)
;
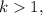правая часть отрицательная, а левая положительна, что не возможно.
;
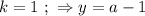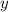его значение 
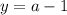и будем искать такие комбинации 
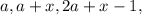чтобы:
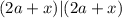– теперь всегда будет выполняться с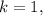 
![( [ a + 1 ] + x ) | ( 3a+x-1 )](/tpl/images/0497/6250/b244e.png)
и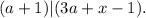
![m ( [ a + 1 ] + x ) = 3a+x-1](/tpl/images/0497/6250/c1228.png)
;![(m-1) x = 3a - 1 - m [ a + 1 ]](/tpl/images/0497/6250/be1b0.png)
;
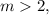правая часть отрицательная, а левая положительна, что не возможно.
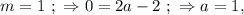но это не подходит по условию.
;
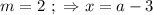его значение 
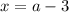и будем искать такие комбинации 
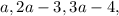чтобы:![( 3 [ a - 1 ] ) | ( 3 [ a - 1 ] )](/tpl/images/0497/6250/de3e6.png)
– теперь всегда будет выполняться с 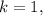![( 2 [ a - 1 ] ) | ( 4 [ a - 1 ] )](/tpl/images/0497/6250/02549.png)
– теперь всегда будет выполняться с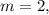 
;
;
;
;
;
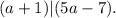
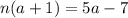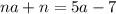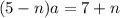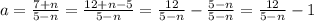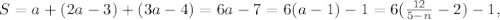
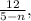т.е. при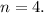 
;
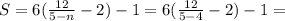
1. 1) -3,4*2,7 = -9,18
2) -1311*(-2221) = 2911731
3) -12,72 : (-0,4) = 127,2 : 4 = 31,8
4) 15,45 : (-15) = -1,03
2. 1) -1,5a*(-6b) = 9ab
2) -4t - 15p + 3t + 18p = -t + 3p
3) b + (7 - b) - (14 - b) = b + 7 - b - 14 + b = b - 7
4) -2(x - 3) + 4(x + 1) = -2x + 6 + 4x + 4 = 2x + 10
3. (-1,14 - 0,96) : (-4,2) + 1,8*(-0,3) = (-2,1) : (-4,2) - 0,54 = 0,5 - 0,54 = -0,04
4. -3*(102x-2) - (4-4,6x) + 6*(0,2x-1) = -306x+6-4+4,6x+1,2x-6 = -300,2x - 4
При x = -1522 получается -300,2*(-1522) - 4 = 456900,4
5. 0,9x - (0,7x + 0,6y) = 0,9x - 0,7x - 0,6y = 0,2x - 0,6y = 0,2*(x - 3y)
Если 3y - x = 9, то x - 3y = -9, тогда выражение равно 0,2*(-9) = -1,8
Пошаговое объяснение:
x=1900/950
x=2
2)10230/x=5115
x=10230/5115
x=2