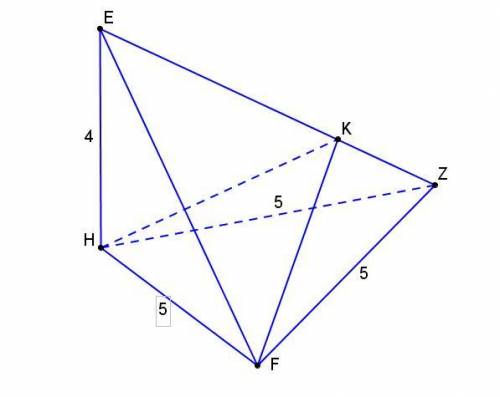
Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.
В данной задаче - это угол FKH.
Отрезки FK и HK это высоты треугольников боковых граней ZEF и HZE.
Находим их длины.
Треугольник ZEF равнобедренный. Боковые стороны равны
FE = ZE = √(5² + 4²) = √(25 + 16) = √41.
Его высота к стороне FZ = √(41 - (5/2)²) = √139/2.
Тогда высота FK к стороне ZE равна (√139/2*5)/√41 = 2,5√(139/41).
Высота НК к стороне EZ равна (4*5)/√41 = 20/√41.
Стороны треугольника HKF определены, по теореме косинусов находим угол HKF.
cos HKF = ((20/√41)² + (2,5√(139/41))² - 5²)/(2*(20/√41)*(2,5√(139/41)) = 0,206746052
Угол HKF равен 1,3626 радиан или 78,0683 градуса.
в первой - 34 карандаша, во второй 17 карандашей, в третьей 85 карандашей.
Пошаговое объяснение:
всего 136 карандашей.
во второй коробке - х карандашей.
в первой коробке в 2 раза больше, значит - 2х карандашей.
в третьей коробке в 5 раз больше, чем во второй, значит - 5х карандашей.
получается, что в трёх коробках х + 2х + 5х = 136 карандашей.
решим уравнение:
х + 2х + 5х = 136
8х = 136
х = 17
Х карандашей было во второй, значит во второй 17.
в первой в два раза больше, чем во второй, значит 17*2=34 карандаша.
в третьей в 5 раз больше, чем во второй, значит 17*5=85 карандашей.