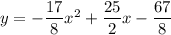
Пошаговое объяснение:
Уравнение параболы в общем виде записывается следующим образом:
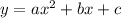
где 
, 
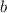и 
-- коэффициенты, которые нам необходимо найти.
Подставим известные нам точки в уравнение параболы и составим систему из трёх уравнений:
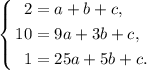
Эту систему можно решать по-разному, дело вкуса. Даю простейшее решение с выражением каждого неизвестного по-очереди.
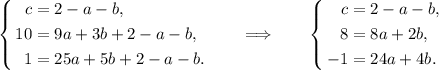
Умножим второе уравнение на 2 и вычтем из третьего второе, чтобы избавиться от :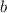
Отсюда видно, что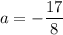 
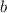, получаем из второго уравнения, а из первого:
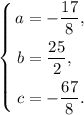
Таким образом, 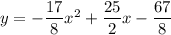- уравнение нашей параболы.
любое целое число a можно представить в виде 3p+r,
где r может принимать лишь значения 0, 1 или 2.
p это какое-то целое число. По сути это деление на 3 с остатком.
Итак, a = 3p+r,
Подставим это значение в исходное выражение:
52a + 112 = 52·(3p+r) + 112 = 3·52·p + 52r + 112.
Эта сумма делится нацело на 3 тогда и только тогда, когда на 3 нацело делится (52r + 112) = R.
Переберём все допустимые значения r.
r = 0, тогда R = 112, на 3 не делится
r = 1, тогда R = 52 + 112 = 164, на 3 не делится.
r = 2, тогда R = 52·2 + 112 = 104 + 112 = 216, делится нацело на 3. Подходит.
ответ. При a = 3p + 2, где p - целое.
1) Раскрываем скобки
- 8у + 8 + 9у - 6 = 0
2) Переносим числа с противоположным знаком в правую часть
- 8у + 9у = 6 - 8
3) Считаем
у = - 2
4) Проверяем
- 4(2*(-2) - 2) + 3 (3*(-2) - 2) = 0
- 4 * (-6) + 3 * (-8) = 0
24 - 24 = 0
0 = 0