Пошаговое объяснение:
№ Уравнение
1 7x + 1 = 15
7х=14
х=2
2 25x - 52 =23
25х=75
х=5
3 6x +11 = 2x - 5
4х=-16
х=-4
4 10 +22,7x = 4,7x +28
18х=18
х=1
5 8,2 - 3x = 11,7 + 2x
-5х=3,5
х=-0,7
6 5 – (x-2) = 4x +17
5-х+2=4х+17
-5х=10
х=-2
7 10x + 2,5 = 12 – (10x – 10,5)
10х+2,5=12-10х+10,5
20х=20
х=1
8 87 – 2x = 2(4x+56)
87-2х=8х+112
-10х=25
х=-2,5
9 3(x + 1 ) + 11 = 34 – 2x
3х+3+11=34-2х
5х=20
х=4
10 4 + 5(2x+1) = 39
4+10х+5=39
10х=30
х=3
11 2x + 8 + x = 13 – x + 19
4х=24
х=6
12 -12(2 – x) = 6x + 48
-24+12х=6х+48
6х=12
х=2
13 35 – 7(5 - x) = x + 12
35-35+7х=х+12
6х=12
х=2
14 49x = 270 – (x + 20)
49х=270-х-20
50х=250
х=5
15 -11x +52 = 46x – (48+ 37x)
-11х+52=46х-48-37х
26х=-100
х=-3,8
16 7,2x – 6 = 2,2x + 14
5х=20
х=4
17 3,6 – 1,2x =1,4x – 1,6
-2,6х=5,2
х=-2
18 1,5 + 5,2x = (4,8x – 1) – 6,7
1,5+5,2х=4,8х-1-6,7
0,4х=-9,2
х=-23
19 850 – 225x = 400
-225х=-450
х=2
20 159x – 21,87 = 84x + 278,13
75х=300
х=4
Пошаговое объяснение:
1)уравнение плоскости Q, проходящей через точки
А (–6; –4; 2);
В (5; –2; –1);
С (5; 6; –4);
для составления уравнения плоскости используем формулу
![\left[\begin{array}{ccc}x-z_A&y-y_A&z-z_A\\x_B-x_A&y_B-y_A&z_B-z_A\\x_C-x_A&y_C-y_A&z_C-z_A\end{array}\right] =0](/tpl/images/1627/6356/c8719.png)
![\left[\begin{array}{ccc}x-(-6)&y-(-4)&z-2\\5-(-5)&(-2)-(-4)&-1-2\\5-(-6)&6-(-4)&-4-2\end{array}\right] =0](/tpl/images/1627/6356/67f4b.png)
(x -(-6))(2*(-6) - (-3)*10) - (y -(-4))(11*(-6) -(-3)*11 ) + (z -2)(11*10 -2*11) = 0
18(x -(-6)) + 33(y - (-4)) + 88(z - 2) = 0
и вот мы получаем уравнение плоскости Q
Q : 18x + 33y + 88z +64 = 0
2) канонические уравнения прямой АВ. А(–6; –4; 2); В(5; –2; –1);
формула канонического уравнения прямой

наша формула прямой
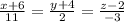
3) уравнение плоскости G, проходящей через точку D(2; 8; 6) перпендикулярно прямой АВ
будем искать прямую в виде 
здесь А, В, С - координаты направляющего вектора.
поскольку G ⊥ АВ, то нормаль АВ будет направляющим вектором для G ⇒ s = n = (11, 2, -3)
и вот формула
G : 11y + 2y - 3z -20 =0
4) расстояние от точки D(2; 8; 6) до плоскости Q : 18x + 33y + 88z +64=0
для расчета нам потребуется
А = 18; В = 33; С = 88; D = 64;
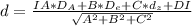
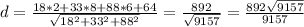
176-5=171
171/6=28,5
28,5+10=38,5
38,5/2=19,25
число 19,25