а) 3000:125=24 карандаша
б) 12кг 600г переводим в граммы
12600:300=42 коробки
Пошаговое объяснение:
В задаче рассматривается множество, в котором 3000 элементов. Это множество разбивается на 125 равночисленных подмножества. Требуется узнать число элементов в каждом таком подмножестве. Это число, как установлено выше, можно найти при деления - 3000:125 . Вычислив значение этого выражения, получаем ответ на вопрос задачи - всего 24 карандаша
В задаче рассматривается множество, в котором 12600 элементов. Это множество разбивается на 300 равночисленных подмножества. Требуется узнать число элементов в каждом таком подмножестве. Это число, как установлено выше, можно найти при деления 12600:300=42 . Вычислив значение этого выражения, получаем ответ на вопрос задачи - всего 42 коробки.
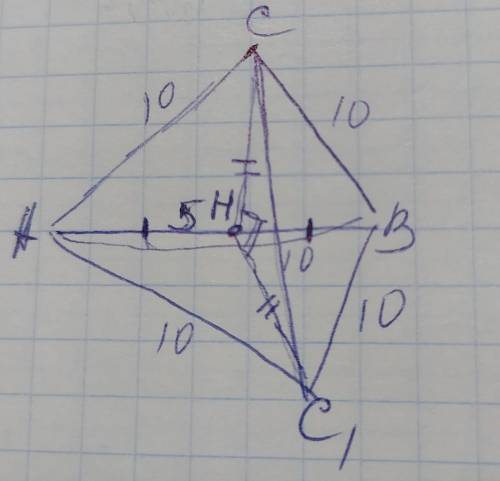
СС1=5√6см
Пошаговое объяснение:
Так как эти треугольники равносторонние и одна общая сторона составляет 10см, то они равны между собой и каждая сторона составит 10см. Проведём из вершин каждого треугольника С и С1 две высоты, которые будут соприкасаться в одной точке Н, и получим высоты СН и СН1. Ввсота в равностороннем треугольнике также является медианой, поэтому обе высоты делят сторону АВ пополам и АН=НВ=10÷2=5см. Рассмотрим полученный ∆АСН. Он прямоугольный где АН и СН катеты, а АС - гипотенуза.. Найдём катет СН по теореме Пифагора:
СН²=АС²–АН²=10²–5²=100–25=75; СН=√75=5√3см
Рассмотрим ∆СС1Н. Он прямоугольный, поскольку плоскости треугольников перпендикулярны, поэтому высоты СН и С1Н также будут перпендикулярны и образуют прямой угол. В ∆СС1Н высоты СН и СН1 являются катетами а СС1 - гипотенуза. Найдём СС1 по теореме Пифагора:
СС1²=СН²+С1Н²=√(75)²+√(75)²=75+75=150;
СС1=√150=√(15×10)=√(25×6)=5√6см
Можно вычислить проще: ∆СС1Н - равнобедренный: СН=С1Н, поскольку если треугольники АВС и АВС1 равны между собой, то и их высоты также равны, а в равнобедренном прямоугольном треугольнике гипотенуза больше катета в √2 раз, поэтому
СС1=СН×√2=5√3×√2=5√6см
c=2*3,14*5=31,4
s=3,14/4*12*12=113,04