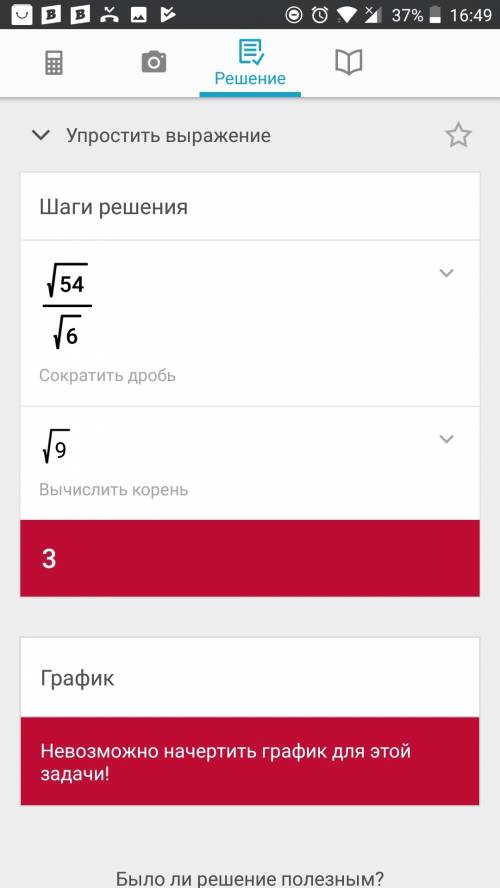
ответ: 1:2:3
Одна сторона треугольника равна 16, а радиус окружности, в которую он вписан - 8. Это значит, что эта сторона является диаметром этой окружности, а треугольник прямоугольный с гипотенузой 16 и одним из катетов 8 квадратных корней из 3.
Второй катет находится по теореме Пифагора: катет равен корню квадратному из разности между квадратоами гипотенузы и второго катета. В нашем случае он равен 8. Мы получили, что второй катет вдвое меньше гипотенузы, значит, угол, ему противолежащий, будет равен 30 градусов, а прилежащий к нему 180 - 30 - 90 = 60 градусов.
Таким образом, дуга деится вершинами треугольника в отношении 90:30:60 = 3:1:2. Или, для удобства записи, 1:2:3.
Разрежем шар вдоль оси конуса... Получим на срезе равнобедренный треугольник вписанный в окружность...
Соединим центр окружности с вершинами треугольника...
Получим еще один треугольник с вершинами в двух точках основания конуса и в центре шара... Этот треугольник равнобедренный со сторонами равными радиусу шара R и высотой равной разности (h-R). Половина его основания вычисляется по теореме Пифагора...
r^2 = R^2 - (h-R)^2 = 2Rh - h^2
1) Если известен радиус шара R=3, то радиус основания конуса равен r = sqrt(6h - h^2)
2) Объем конуса равен 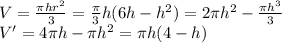
Функция обема конуса возрастает при h<4 и убывает при h>4
Следовательно максимальный объем будет при h=4