Если все боковые рёбра пирамиды равны, то основанием её высоты будет центр описанной окружности у основания. У прямоугольника это точка пересечения его диагоналей.
Найдём высоту (h), как катет одного из 4 равных прямоугольных треугольников, с гипотенузой соответствующей боковому ребру пирамиды и с катетом соответствующему половине диагонали прямоугольника (в прямоугольники диагонали делятся точкой пересечения пополам).
Диагональ основания (d) найдём, как гипотенузу одного из двух равных прямоугольных треугольников, которые образуются при проведении одной диагонали.
d = √(18²+24²) = 6√(3²+4²) = 6√25 = 6·5 = 30см
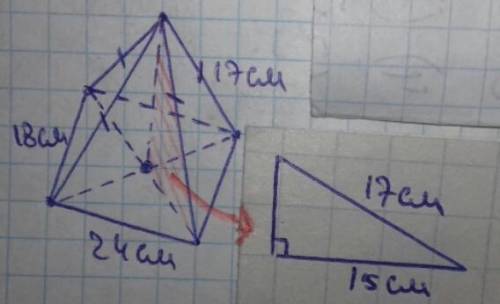
d/2 = 30:2 = 15см
h = √(17²-15²) = √(289-225) = √64 = 8см
ответ: 8см.
100-60=40-5=35