Утрапеції abcd відомо,що bc||ad, bc = 3 см,аd = 10 см, сd = 4 см, кут d = 60°.знайдіть діагоналі трапеції.

Question

Математика: Утрапеції abcd відомо,що bc||ad, bc = 3 см,аd = 10 см, сd = 4 см, кут d = 60°.знайдіть діагоналі трапеції.​

PollinaKipollina24 · Accepted Answer

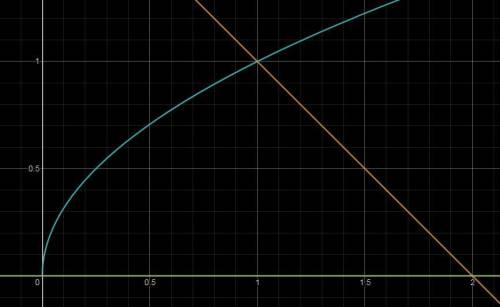
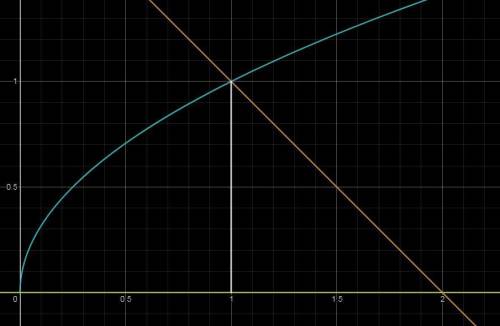
Построим все эти графики в одной системе координат (см. вложение №1). Получившаяся фигура не является криволинейной трапецией, но, проведя прямую 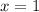x = 1 (см. вложение №2), можно разбить её на две криволинейные трапеции, у каждой из которых можно найти площадь. Искомая площадь является суммой площадей двух составляющих эту фигуру криволинейных трапеций.

Итак, находим площадь левой криволинейной трапеции.

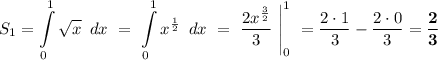
$\displaystyle S_1 = \int\limits_0^1 \sqrt{x}\,\ dx\ =\ \int\limits_0^1x^{\frac{1}{2}}\,\ dx\ =\ \dfrac{2x^\frac{3}{2}}{3}\ \Bigg|_0^1\ = \dfrac{2\cdot 1}{3} - \dfrac{2\cdot 0}{3} = \bf{\dfrac{2}{3}}$

Теперь находим площадь правой криволинейной трапеции.

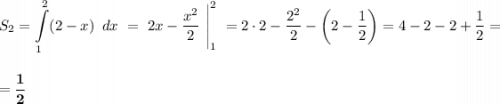
$\displaystyle S_2 = \int\limits_1^2(2-x)\,\ dx\ =\ 2x - \dfrac{x^2}{2}\ \Bigg|_1^2\ =2\cdot 2 - \dfrac{2^2}{2} - \left(2 - \dfrac{1}{2}\right) = 4 - 2 - 2 +\dfrac{1}{2} =\\\\\\= \bf{\dfrac{1}{2}}$

А теперь складываем и находим искомую площадь.

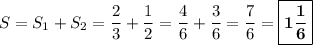$S = S_1 + S_2 = \dfrac{2}{3} + \dfrac{1}{2} = \dfrac{4}{6} + \dfrac{3}{6} = \dfrac{7}{6} = \boxed{\bf{1\dfrac{1}{6}}}$ .

ответ: 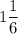$1\dfrac{1}{6}$ .

Найдите площадь фигуры ограниченной графиками функций: , y=2-x, y=0, через интегрирование

Утрапеції abcd відомо,що bc||ad, bc = 3 см,аd = 10 см, сd = 4 см, кут d = 60°.знайдіть діагоналі трапеції.​

MOGZ ответил